Curriculum Learning
28 Jun 2019 | Deep_Learning HS
이번에도 재미있는 공부거리를 들고 왔습니다. Active Learning 에 이어서, 효율적인 머신 러닝 학습을 가능케하는 방법론인 Curriculum learning 에 대한 논문에 대해 이야기해보려 합니다. 이번에 포스팅할 논문은 2009년에 Y.Bengio 교수님이 쓰신 “Curriculum Learning” 이라는 논문입니다. 커리큘럼 러닝(CL이라고 쓰겠습니다!) 에 시발점과 같은 논문이니, 흥미롭게 봐주셨으면 좋겠습니다!
머신러닝 모델을 학습시킬 때, 데이터가 너무 클 경우 사용자는 데이터를 배치로 잘라서 넣곤 하는데, 이 때 데이터의 순서에 대해서는 큰 생각을 하지 않습니다. 즉, 랜덤하게 넣게 되는 것이죠. 하지만 모델은 데이터를 순차적으로 받게 되고 이렇게 받는 데이터에 따라 조금씩 학습을 합니다.
인간이 학습을 하는 프로세스를 떠올려보면, 고등학교까지 20년의 고등 교육을 받으면서 저희가 초등학교 때 배운 내용과 수능 공부가 과연 같은 난이도를 가지고 있을까요? 아니죠! 저희는 점차 학습을 해나가면서 똑똑해지고, 더 어려운 공부 내용을 받아드려질 준비를 점차 해나가면서 보다 어려운 학습을 수행하게 됩니다.
CL은 위와 같은 아이디어 아래에서 모델에게 데이터를 주고 학습시킬 때, 랜덤한 순서로 주는 것이 아닌 처음에는 쉬운 것부터 시작해서 점차 어려운 데이터를 주면서 학습시켜 나가자! 라는 방법론을 제시합니다.
이러한 방법론을 머신 러닝에 사용한 결과, 학습 효율이 높아져 수렴 속도가 빨라지고, local minima 에 빠지는 경향성이 줄어들어 효율적이고 고성능의 성과를 낼 수 있었다고 합니다.
해당 논문에서는 non-convex 한 조건에서의 최적화 방법인 continuation method 와 커리큘럼의 아이디어를 연관지어 설명합니다. continuation method 에서는 보다 global minima 를 찾기 위해서, 처음에는 미지의 식에 대한 smooth version 을 제시하여,(regularization term이 큰 것으로 생각할 수 있습니다) 최대한 convex 하게 만들어 global picuture를 본다라고 합니다. 처음부터 노이즈일 수도 있는 부분을 보기보다는 미지의 식을 나이브하게 구축하여, “대충 이렇게 생겼구나~” 라는 개요를 가지고 온 후, 점점 복잡한 디테일들을 다루게 되는 것입니다.
위의 식에서 $P(z)$ 는 데이터의 분포입니다. 즉, 사용자가 예측하려는 패턴이 있는 곳이며, 함수로 표현하려고 하는 대상이 됩니다. $W_{\lambda}(z)$ 는 프로세스가 얼마나 진행되었는지를 비율의 형태로 표현하는 것으로 1이 되면, 전체 프로세스(커리큘럼)가 끝나는 것을 의미합니다. 이에 따라서 모든 프로세스가 끝나면, 사용자가 최적화하려는 대상은 실제 데이터의 분포가 같게 됩니다.
커리큘럼이 진행됨에 따라, 모델이 학습하는 데이터의 난이도가 올라가는 것은 정보량의 관점으로도 이해할 수 있습니다.
저자는 논문 내에서 shape recognition 이라는 테스크를 진행하였는데, 예시 데이터는 아래와 같습니다.

위의 사진이 아래의 사진보다 상대적으로 안에 있는 도형이 삼각형인지 원인지 인식하는 것이 쉽습니다. 저자는 쉬운 데이터를 따로 모아 (이부분에서 실험자의 사전 정보를 넣게 됩니다.) 순서대로 모델에 넣어 학습시킵니다.
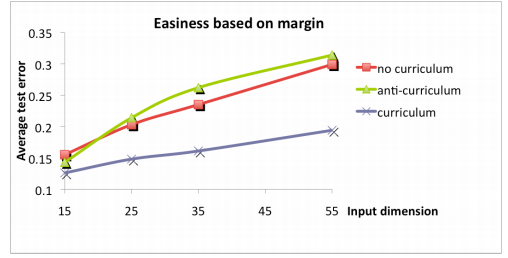
결과는 위의 사진과 같고, 빨리 수렴하며 loss 가 상대적으로 적은 것을 알 수 있습니다. 해당 논문의 주요 논점은 CL을 제시 및 정리하였고, 실험자(instructor)의 사전 정보(prior information)을 통해서 쉬운 데이터를 선별하고 순차적으로 학습시켰다는 것에 있습니다.
이번에도 재미있는 공부거리를 들고 왔습니다. Active Learning 에 이어서, 효율적인 머신 러닝 학습을 가능케하는 방법론인 Curriculum learning 에 대한 논문에 대해 이야기해보려 합니다. 이번에 포스팅할 논문은 2009년에 Y.Bengio 교수님이 쓰신 “Curriculum Learning” 이라는 논문입니다. 커리큘럼 러닝(CL이라고 쓰겠습니다!) 에 시발점과 같은 논문이니, 흥미롭게 봐주셨으면 좋겠습니다!
머신러닝 모델을 학습시킬 때, 데이터가 너무 클 경우 사용자는 데이터를 배치로 잘라서 넣곤 하는데, 이 때 데이터의 순서에 대해서는 큰 생각을 하지 않습니다. 즉, 랜덤하게 넣게 되는 것이죠. 하지만 모델은 데이터를 순차적으로 받게 되고 이렇게 받는 데이터에 따라 조금씩 학습을 합니다.
인간이 학습을 하는 프로세스를 떠올려보면, 고등학교까지 20년의 고등 교육을 받으면서 저희가 초등학교 때 배운 내용과 수능 공부가 과연 같은 난이도를 가지고 있을까요? 아니죠! 저희는 점차 학습을 해나가면서 똑똑해지고, 더 어려운 공부 내용을 받아드려질 준비를 점차 해나가면서 보다 어려운 학습을 수행하게 됩니다.
CL은 위와 같은 아이디어 아래에서 모델에게 데이터를 주고 학습시킬 때, 랜덤한 순서로 주는 것이 아닌 처음에는 쉬운 것부터 시작해서 점차 어려운 데이터를 주면서 학습시켜 나가자! 라는 방법론을 제시합니다.
이러한 방법론을 머신 러닝에 사용한 결과, 학습 효율이 높아져 수렴 속도가 빨라지고, local minima 에 빠지는 경향성이 줄어들어 효율적이고 고성능의 성과를 낼 수 있었다고 합니다.
해당 논문에서는 non-convex 한 조건에서의 최적화 방법인 continuation method 와 커리큘럼의 아이디어를 연관지어 설명합니다. continuation method 에서는 보다 global minima 를 찾기 위해서, 처음에는 미지의 식에 대한 smooth version 을 제시하여,(regularization term이 큰 것으로 생각할 수 있습니다) 최대한 convex 하게 만들어 global picuture를 본다라고 합니다. 처음부터 노이즈일 수도 있는 부분을 보기보다는 미지의 식을 나이브하게 구축하여, “대충 이렇게 생겼구나~” 라는 개요를 가지고 온 후, 점점 복잡한 디테일들을 다루게 되는 것입니다.
위의 식에서 $P(z)$ 는 데이터의 분포입니다. 즉, 사용자가 예측하려는 패턴이 있는 곳이며, 함수로 표현하려고 하는 대상이 됩니다. $W_{\lambda}(z)$ 는 프로세스가 얼마나 진행되었는지를 비율의 형태로 표현하는 것으로 1이 되면, 전체 프로세스(커리큘럼)가 끝나는 것을 의미합니다. 이에 따라서 모든 프로세스가 끝나면, 사용자가 최적화하려는 대상은 실제 데이터의 분포가 같게 됩니다.
커리큘럼이 진행됨에 따라, 모델이 학습하는 데이터의 난이도가 올라가는 것은 정보량의 관점으로도 이해할 수 있습니다.
저자는 논문 내에서 shape recognition 이라는 테스크를 진행하였는데, 예시 데이터는 아래와 같습니다.

위의 사진이 아래의 사진보다 상대적으로 안에 있는 도형이 삼각형인지 원인지 인식하는 것이 쉽습니다. 저자는 쉬운 데이터를 따로 모아 (이부분에서 실험자의 사전 정보를 넣게 됩니다.) 순서대로 모델에 넣어 학습시킵니다.

결과는 위의 사진과 같고, 빨리 수렴하며 loss 가 상대적으로 적은 것을 알 수 있습니다. 해당 논문의 주요 논점은 CL을 제시 및 정리하였고, 실험자(instructor)의 사전 정보(prior information)을 통해서 쉬운 데이터를 선별하고 순차적으로 학습시켰다는 것에 있습니다.
Comments