의사 결정 나무 (Decision Tree)
03 Jan 2019 | Machine_Learning HS
본 포스팅은 카이스트 문일철 교수님의 강좌를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
분류 문제에 대한 첫 번째 알고리즘 의사 결정 트리(Decision Tree) 에 대해서 이야기해보려 합니다. 의사 결정 트리는 분류 문제 뿐만 아니라 회귀 문제에도 적용될 수 있기 때문에, CART(Classification And Regression Tree)라고도 합니다.
분류란? (Classification)
위키피디아에 따르면, 머신 러닝에서 분류란 statistical Classification 으로 세분화될 수 있고, 이는 새로운 관측 데이터(트레이닝 데이터)를 카테고리 세트 중 하나로 인식하는 것을 의미합니다. (identifying to which of a set of categories a new observation belongs, on the basis of a training set of data)
좀 더 머신 러닝 알고리즘에 직관적인 해석을 빌려볼까요? 김도형 박사님의 블로그에 따르면,
분류(classification)는 독립 변수 값이 주어졌을 때
그 독립 변수 값과 가장 연관성이 큰 종속변수 카테고리(클래스)를 계산하는 문제이다.
즉, X(입력 데이터)를 넣으면, 회귀식처럼 연속적인 결과값이 나오는 것이 아닌, 이들의 패턴이나 특성에 따라서 클래스(K)의 규모에 따라, 이산적이고 bounded한 값을 반환하는 문제를 의미합니다.
이제 본격적으로 의사 결정 나무(Decision Tree)에 대해서 이야기해보겠습니다.
## What is for Entropy?
우선, 의사 결정 나무가 어떻게 형성되어 있는지 한 번 볼까요?
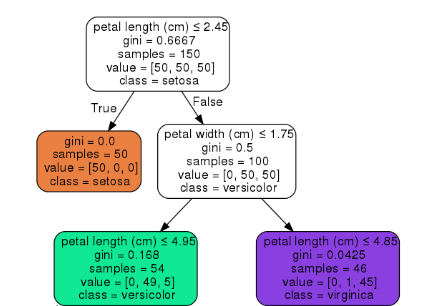
부모 노드에서 자식 노드로 내려가면서 데이터(입력 변수)가 세분화되어 가는 것을 보실 수 있습니다. 엔트로피는 이렇게 세분화되어 가는 과정에서 기준이 됩니다.
엔트로피란?
-
불확실성(uncertainty)를 측정(measure)하는 수단으로, 엔트로피가 높을 수록, 불확실성이 높아집니다.(Higher entropy means more uncertainty)
-
수식으로 보면 아래와 같습니다.
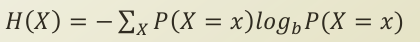
P(X=x)는 [0,1]값을 가지고 있기 때문에, log(P(X=x)) 값은 음수가 됩니다. log function의 형태적 특징상, 0에 근접할 수록, 기하급수적으로 값이 작아지게 되고, 1이 되면, 그 값이 0이 됩니다. 또한, 로그 연산 앞에 P(X=x)를 곱해주었기 때문에, 자기 자신의 확률로 곱한 값이 됩니다. 이러한 특성에 따라, 상반된 두 확률의 경우를 보게 되면, 아래와 같습니다.
[1.0,0.0](certainty) -> H(X) = 0(min)
[0.5,0.5](uncertainty) -> H(X) = 1(max)
또한, 의사 결정 나무의 분류 기준을 이해하기 위해서는 조건부 엔트로피(conditional entropy)를 이해해야 합니다.
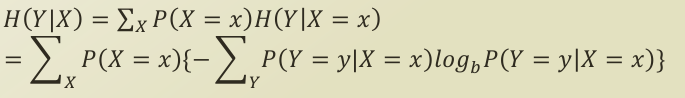
H(Y|X) 를 어떻게 해석할 수 있을까요?
- 주어진 특징 변수 X에 따른 클래스 Y에 대한 엔트로피
- 자식 노드가 어떻게 분류되는 지에 따른, 부모 노드의 엔트로피 변화
의사결정나무의 노드가 내려가면서, 분류기는 입력 변수 데이터들이 분명하게 분류되면서 하위 노드로 가게끔 설계됩니다. 분명하게 분류된다는 것은 확실성(certainty)가 높다는 이야기이고, 부모 노드와 자식 노드 간 엔트로피 차이를 작게 한다는 이야기가 됩니다.(low H(Y|X))
정보 획득량(Information Gain)
부모 노드 Y가 자식 노드 X에 의해서 엔트로피가 얼마나 감소하였는지를 나타내는 값으로써, 통상 IG라고 씁니다.

위에서 다뤘던 IG에 따라 노드가 하위 노드로 내려가면서(입력 변수의 클래스에 따른 세분화) performance 와 over-fitting 방지를 위한 max-depth 조건을 생각하지 않았을 경우, 일정 노드가 한 쪽 클래스에만 존재하게 되었을 때, 해당 노드는 중지되고, 전체 노드가 해당 조건을 따랐을 때, 모델이 종료됩니다.
본 포스팅은 카이스트 문일철 교수님의 강좌를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
분류 문제에 대한 첫 번째 알고리즘 의사 결정 트리(Decision Tree) 에 대해서 이야기해보려 합니다. 의사 결정 트리는 분류 문제 뿐만 아니라 회귀 문제에도 적용될 수 있기 때문에, CART(Classification And Regression Tree)라고도 합니다.
분류란? (Classification)
위키피디아에 따르면, 머신 러닝에서 분류란 statistical Classification 으로 세분화될 수 있고, 이는 새로운 관측 데이터(트레이닝 데이터)를 카테고리 세트 중 하나로 인식하는 것을 의미합니다. (identifying to which of a set of categories a new observation belongs, on the basis of a training set of data) 좀 더 머신 러닝 알고리즘에 직관적인 해석을 빌려볼까요? 김도형 박사님의 블로그에 따르면,
분류(classification)는 독립 변수 값이 주어졌을 때
그 독립 변수 값과 가장 연관성이 큰 종속변수 카테고리(클래스)를 계산하는 문제이다.
즉, X(입력 데이터)를 넣으면, 회귀식처럼 연속적인 결과값이 나오는 것이 아닌, 이들의 패턴이나 특성에 따라서 클래스(K)의 규모에 따라, 이산적이고 bounded한 값을 반환하는 문제를 의미합니다.
이제 본격적으로 의사 결정 나무(Decision Tree)에 대해서 이야기해보겠습니다.
## What is for Entropy?
우선, 의사 결정 나무가 어떻게 형성되어 있는지 한 번 볼까요?

부모 노드에서 자식 노드로 내려가면서 데이터(입력 변수)가 세분화되어 가는 것을 보실 수 있습니다. 엔트로피는 이렇게 세분화되어 가는 과정에서 기준이 됩니다.
엔트로피란?
-
불확실성(uncertainty)를 측정(measure)하는 수단으로, 엔트로피가 높을 수록, 불확실성이 높아집니다.(Higher entropy means more uncertainty)
-
수식으로 보면 아래와 같습니다.
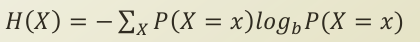
P(X=x)는 [0,1]값을 가지고 있기 때문에, log(P(X=x)) 값은 음수가 됩니다. log function의 형태적 특징상, 0에 근접할 수록, 기하급수적으로 값이 작아지게 되고, 1이 되면, 그 값이 0이 됩니다. 또한, 로그 연산 앞에 P(X=x)를 곱해주었기 때문에, 자기 자신의 확률로 곱한 값이 됩니다. 이러한 특성에 따라, 상반된 두 확률의 경우를 보게 되면, 아래와 같습니다.
[1.0,0.0](certainty) -> H(X) = 0(min)
[0.5,0.5](uncertainty) -> H(X) = 1(max)
또한, 의사 결정 나무의 분류 기준을 이해하기 위해서는 조건부 엔트로피(conditional entropy)를 이해해야 합니다.
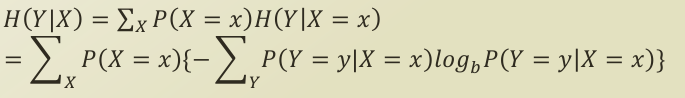
H(Y|X) 를 어떻게 해석할 수 있을까요?
- 주어진 특징 변수 X에 따른 클래스 Y에 대한 엔트로피
- 자식 노드가 어떻게 분류되는 지에 따른, 부모 노드의 엔트로피 변화
의사결정나무의 노드가 내려가면서, 분류기는 입력 변수 데이터들이 분명하게 분류되면서 하위 노드로 가게끔 설계됩니다. 분명하게 분류된다는 것은 확실성(certainty)가 높다는 이야기이고, 부모 노드와 자식 노드 간 엔트로피 차이를 작게 한다는 이야기가 됩니다.(low H(Y|X))
정보 획득량(Information Gain)
부모 노드 Y가 자식 노드 X에 의해서 엔트로피가 얼마나 감소하였는지를 나타내는 값으로써, 통상 IG라고 씁니다.

위에서 다뤘던 IG에 따라 노드가 하위 노드로 내려가면서(입력 변수의 클래스에 따른 세분화) performance 와 over-fitting 방지를 위한 max-depth 조건을 생각하지 않았을 경우, 일정 노드가 한 쪽 클래스에만 존재하게 되었을 때, 해당 노드는 중지되고, 전체 노드가 해당 조건을 따랐을 때, 모델이 종료됩니다.
Comments