가우시안 혼합 모형, K-Means Algorithm
20 Feb 2019 | Machine_Learning HS
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
K-Means Algorithm
K 개의 센트로이드(centroid)를 정하고, 센트로이드와 떨어진 정도에 따라, 클러스터링을 하는 알고리즘을 의미합니다.

위의 이미지에서 각각의 term들이 의미하는 바를 살펴봅시다.
- N : 데이터(observations)의 갯수
- K : 클래스 또는 센트로이드(centroid)의 갯수
- r_nk : 해당 클래스 k에 해당하는 데이터인지에 대한 할당 계수 {0,1}
- x_n : n번째 데이터(observations)
- Mu_k : k번째 센트로이드
각각의 term들이 어떤 것인지 파악한 상태에서 위의 식을 다시 살펴보면, 센트로이드와 각각의 데이터 셋들의 거리(distance)를 계산해 더하는 것이 되겠습니다. 또한, 할당 계수를 통해서 해당 시점에서 정해진 센트로이드에 따라, 특정 클러스터에 속한 데이터 셋의 거리만 연산이 되게끔 되는 것이죠.
K-means 알고리즘에서는 결과적으로 최적의 센트로이드(optimal centriod)를 찾는 것이 관건이 됩니다. 하지만, 아시다시피 비지도학습(un-supervised learning)이라는 특징을 가지고 있기 때문에, 라벨 데이터가 아닌 iterative process 를 거쳐서 최적의 값에 근사하게끔 해주어야 합니다.
그에 따라 나오는 알고리즘이 Gaussian Mixture model 입니다.
Gaussian Mixture Model
Multinomial Distribution
강의의 순서에 맞춰 Multinomial Distribution부터 다뤄보도록 하겠습니다. 다항 분포라 불리는 이 분포는 이전 포스팅에서도 간략하게 다룬 적이 있지만, 후에 나올 EM 방법에서 접목되기 때문에, 해당 포스팅에서는 pdf 를 보다 깊이 다뤄보도록 하겠습니다.

pdf함수는 위의 이미지와 같습니다. 수식으로 되어 가독성이 떨어지지만 저희가 쉽게 다가갈 수 있는 예제로 이해해보면,(주사위 던지기) 당연한 계산 방법이 됩니다.
중요한 것은 파라미터에 붙는, 부등식 , 등식 제약식(constraint)에 대한 부분입니다. 이에 따라서, argmax_μ [P(X
μ)] 와 같은 식에서 X를 다항 분포를 가정할 때, 부등식 제약 조건에서의 최적화를 실시해야 합니다. (Lagrange method)

Multivariate Gaussian Distribution

다변량 정규분포의 최적화를 위해서는 trace trick 이라는 트릭을 사용해야 하는데, 강의에서는 다루지 않았기 때문에, 본 포스팅에서도 생략하도록 하겠습니다.

Mixture Model
쌍봉 낙타의 등 같은 히스토그램이 있을 때, 이러한 분포에 대해서 단일 정규 분포로 표현하는 것은 무리가 있습니다. 즉, 설명력이 떨어질 수 있습니다. 이러한 경우, 2개 이상의 정규 분포가 혼합(mix)되어 있는 형태라고 표현하는 것을 Mixture model 이라고 합니다.

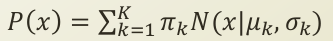
위의 식들의 term들을 살펴보면, 아래와 같습니다.
- π_k : 여러 정규분포들의 가중합에서 가중치를 나타냄.
- 0 <= π_k <= 1
- 확률(probability)의 형태
- 새로운 변수로써 Z라고 칭합니다.
-
N(x
μ_k , σ_k) : k번째 정규 분포(subpopulation이라 칭함)의 pdf함수
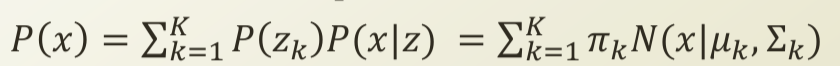
위에서 확률값의 형태를 지니는 새로운 변수 π_k 의 형태를 조금 변형해, P(z_k)로 하자고 했으므로, 위와 같은 등식이 성립됩니다. z_k에 따라서, 다수의 정규 분포들이 혼합되게 되는 것이죠. Mixing coefficient 또는 Selection variable 이라고 부릅니다.
z_k 의 특징에 대해, 다시 짚고 넘어가 보면, 각각은 확률값을 띄고, {0,1}의 확률 변수값만 지닙니다. 예로 들어서, P(z_k = 1 ) = π_k 이다. 와 같은 것이죠. 즉, π_k는 확률값 그 자체이고, z_k 은 확률 변수 값이 됩니다. 만약 k가 3이면,
P(z_1 = 1 ) = π_1
P(z_2 = 1 ) = π_2
P(z_3 = 1 ) = π_3
P(Z) = π_1*(1-π_1)*π_2*(1-π_2)*π_3*(1-π_3)
Multinomial distribution의 형태가 된다.
나머지 term(normal distribution pdf function)은 그대로 곱셈 연산이 적용됩니다.


바로 위에 나오는 이미지는 marginalized probability라고 불리는 부분입니다. 즉, 위에서 π_k와 같은 확률값 그 자체를 z_k라는 확률 변수 형태로 바뀌줌으로써, P(z_k)를 풀어나가면서, multinomial distribution이라는 결론에 도달하였는데, 이번에는 데이터(observations)라는 sub_term을 추가해 z_nk로 만들어주고 rho function를 씌워줌으로써, x_n 라는 데이터가 k번째 mixture distribution에 속할 확률 이라는 개념을 만들어냈습니다. 우변의 분모는 marginalize out 시켜주기 위해서 모든 k의 경우를 더한 것이고, 분자는 k의 경우만 나타낸 것이 되겠습니다.
맨 처음에 K-Means Algorithm을 다루다가 갑자기 왜 Gaussian Mixture Model 이 나오고, 거기에 더해서 복잡한 식들과 합께, 특정 데이터가 특정 mixture distribution에 속할 확률을 알아야 할까요?! 그 이유는 바로 GMM 와 K-Means 알고리즘 사이의 유사성에 기인합니다.
- 두 알고리즘 모두 두 개의 상호작용하는 파라미터들을 가지고 있습니다.
- K-Means 의 경우 할당 계수(r_nk) 와 센트로이드(Mu_k)
- GMM 의 경우, normal distribution의 parameter 와, 가중치 계수
- EM(Expectation - Maximization) 방법을 사용해서 최적화합니다.
- Expectation : 클러스터들과 데이터 점들 사이의
할당
- Maximization : 파라미터
업데이트
Expectation step

처음이면 arbitrary parameter x, π, μ, Σ 에 따라서,rho(z_nk)를 계산합니다.
rho(z_nk)를 통해서, assignment probability를 계산할 수 있게 됩니다. 이에 따라서, 가장 가까운 클러스터에 데이터를 할당합니다. 이렇게 계산된 rho(z_nk)는 새로운 파라미터를 업데이터하는 데에 사용됩니다.
Maximization step

위의 식은 이전에 계산했던, multinomial distribution 의 최적화한 값과, Multivariate normal distribution 의 최적화한 값을 적용한 것에 따른 것입니다. 전체적인 계산 과정에 대한 별다른 언급은 생략하겠으나, 하나만 다뤄보면, 마지막 두 번째 줄의 우변에서, {} 내부 항의 첫 번째 항의 합(n=1 -> N)을 계산해보면, N * (1/K) 정확히 같지는 않겠지만, marginal out 되어 있는 상태입니다. 이 됩니다. 하지만, 이때 외부 항에 있는 합(k=1 -> K)을 대입하면, N * K * (1/K) = N이 됩니다. 이에 따라, Lagrange method 의 lambda 는 -N이라는 결론에 다다릅니다. 결과적으로 π_k의 optimal(updated)값을 알 수 있게 됩니다.
Relation between K-Means and GMM
GMM 와 K-Means 두 알고리즘 사이의 차이는 각각의 Mixture model의 distribution의 분산이 같은지 다른지에 대한 것입니다. 즉, GMM의 경우 존재하는, 공분산 행렬이 K-Means Algorithm에서는 모든 distribution 의 분산을 같다고 가정하면서, e * Identity matrix로 표현하게 되는 것입니다. 이에 따라서, EM 최적화 프로세스 과정이 구분됩니다.

Expectation - Maximization
K-Means Algorithm 에서 EM 방법이 쓰이는 이유는, 비지도 학습이기 때문임을 넘어서, interactive parameter를 가지고 있기 때문입니다. 즉, 하나의 파라미터가 변화함에 따라, 다른 파라미터가 영향을 받아 최적화 과정에서 그 움직임이 변화하며, 복수 개의 파라미터가 최적점을 찾아가는 과정(iterative process)에 EM 방법이 쓰이는 것이죠.
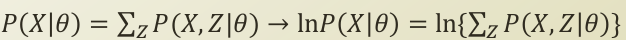
위의 식들을 순서대로, 나열해보면 다음과 같습니다.
-
P(X
θ) = SUM_z(P(X,Z
θ)) : latent variable Z 가 추가되면서, marginal out 시킴으로써 양변을 같게 만듭니다.
-
ln(P(X
θ)) = ln(SUM_z(P(X,Z
θ))) : 양변에 자연로그를 씌워줍니다.
자연로그를 취해줌으로써, monotonous를 유지하면서, 미분을 편하게 하려 했지만, 내부 항에 있는 Summation으로 인해, 계산이 복잡해졌습니다. 이에 따라, E 과정 M 과정을 통해, 자체적으로 최적화를 실시합니다.
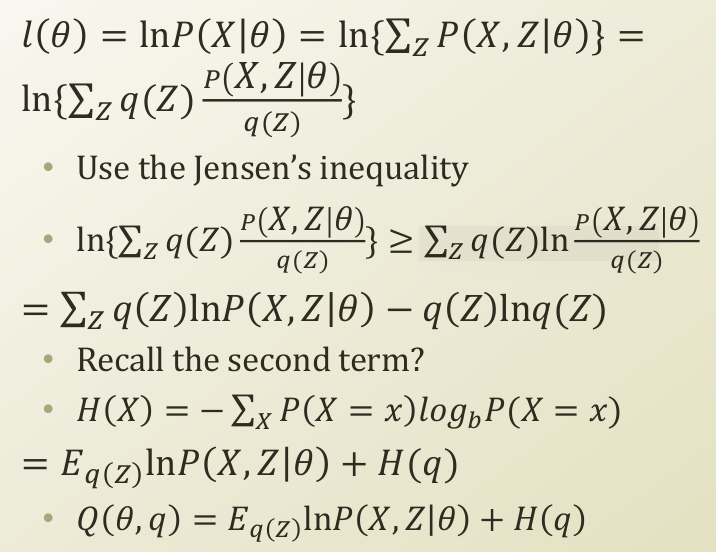
우리가 계산하려는, log likelihood 는 일단, log 함수입니다. log 함수는 concave 함수입니다.
Jensen’s inequality를 맞춰주기 위해서, q(Z) term을 의도적으로 추가해주고, 부등식을 만들어줍니다.
부등식이 성립하는 대신, SUM_z가 자연 로그 항에서 빠져나오게 되었습니다.
빠져나옴으로써, 계산이 편해진 우변을 계속해서 분해해보면,
SUM_z(q(Z)ln(P(X,Z|θ) - q(Z)ln(q(Z)))) 항이 됩니다.
-q(Z)ln(q(Z)) 에서 q(Z)를 확률의 형태로 해석하면 entropy의 식과 같아집니다.
분해한 좌변의 머리부분에 E_q(Z)가 갑자기 씌워졌는데, q(Z)를 확률의 형태로 해석하면서, 가중 평균(weighted average)가 되면서 씌워진 것입니다.
이렇게 재해석한 분해값들의 합을 Q(θ|q)라고 부르도록 합니다.
중요한 부분을 놓칠 뻔 했는데요. 저희가 구한 Q(θ
q) 값은 실제 log likelihood의 lower bound 입니다.
즉, 실제 값은 Q(θ
q)보다 크다는 것이죠. 이에 따라서, 실제 값과 근사하게 하기 위해서는 Q(θ
q)를 극대화(Maximizing)하면 됩니다.

극대화를 위해, 식을 이리저리 재조립(rearrange)을 해봅니다. 위의 이미지의 마지막 식에서 유레카가 나옵니다! ln(P(X
θ)) - SUM_z{q(Z)ln(q(Z) / P(Z
X,θ))} 부분이 나오는데, 이 식의 좌변은 저희가 원래 구하려고 한, latent variable 이 있는 그 log likelihood입니다. 우변의 마이너스 term 으로 인해 inequality가 성립함을 알 수 있습니다.

마지막 항을 딥러닝의 loss function으로 많이 사용되는 cross_entropy 와 긴밀히 연관된 kull-back leiber 입니다. 두 확률 분포의 유사성에 대한 지표로 사용되며, 유사할 수록 그 값은 0으로 작아집니다.

저희는 Q(θ,q)를 최대화시킴으로써, L(θ,q)를 최소화시킴으로써, 실제 값에 가까워질 수 있습니다. 하지만 Q(θ,q) 식에서, q(Z)에 대한 정보가 없습니다. 즉, L(θ,q)를 통해 알아내야 하는 것이죠. 이에 따라서, L(θ,q)를 최소화하는 최적화를 통해 q_t(z) 를 구하고, 그렇게 최적화된, q(z_t)를 Q(θ,q)에 집어 넣는 것이죠. 이번에는 업데이트된 q_t(z)를 통해, θ_t를 업데이트합니다. 그 후, 다시 L(θ,q)로 가서 새로운 q_{t+1}을 찾는 것이죠.
- L(θ,q)에서 q_t를 찾는다 -> Expectation step
- Q(θ,q)에서 θ_t를 찾는다 -> Maximiation step

위와 같은 EM looping 을 수렴할 때까지(KL가 0으로 수렴할 때까지) 실행하게 됩니다.
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
K-Means Algorithm
K 개의 센트로이드(centroid)를 정하고, 센트로이드와 떨어진 정도에 따라, 클러스터링을 하는 알고리즘을 의미합니다.

위의 이미지에서 각각의 term들이 의미하는 바를 살펴봅시다.
- N : 데이터(observations)의 갯수
- K : 클래스 또는 센트로이드(centroid)의 갯수
- r_nk : 해당 클래스 k에 해당하는 데이터인지에 대한 할당 계수 {0,1}
- x_n : n번째 데이터(observations)
- Mu_k : k번째 센트로이드
각각의 term들이 어떤 것인지 파악한 상태에서 위의 식을 다시 살펴보면, 센트로이드와 각각의 데이터 셋들의 거리(distance)를 계산해 더하는 것이 되겠습니다. 또한, 할당 계수를 통해서 해당 시점에서 정해진 센트로이드에 따라, 특정 클러스터에 속한 데이터 셋의 거리만 연산이 되게끔 되는 것이죠.
K-means 알고리즘에서는 결과적으로 최적의 센트로이드(optimal centriod)를 찾는 것이 관건이 됩니다. 하지만, 아시다시피 비지도학습(un-supervised learning)이라는 특징을 가지고 있기 때문에, 라벨 데이터가 아닌 iterative process 를 거쳐서 최적의 값에 근사하게끔 해주어야 합니다.
그에 따라 나오는 알고리즘이 Gaussian Mixture model 입니다.
Gaussian Mixture Model
Multinomial Distribution
강의의 순서에 맞춰 Multinomial Distribution부터 다뤄보도록 하겠습니다. 다항 분포라 불리는 이 분포는 이전 포스팅에서도 간략하게 다룬 적이 있지만, 후에 나올 EM 방법에서 접목되기 때문에, 해당 포스팅에서는 pdf 를 보다 깊이 다뤄보도록 하겠습니다.

pdf함수는 위의 이미지와 같습니다. 수식으로 되어 가독성이 떨어지지만 저희가 쉽게 다가갈 수 있는 예제로 이해해보면,(주사위 던지기) 당연한 계산 방법이 됩니다.
| 중요한 것은 파라미터에 붙는, 부등식 , 등식 제약식(constraint)에 대한 부분입니다. 이에 따라서, argmax_μ [P(X | μ)] 와 같은 식에서 X를 다항 분포를 가정할 때, 부등식 제약 조건에서의 최적화를 실시해야 합니다. (Lagrange method) |

Multivariate Gaussian Distribution

다변량 정규분포의 최적화를 위해서는 trace trick 이라는 트릭을 사용해야 하는데, 강의에서는 다루지 않았기 때문에, 본 포스팅에서도 생략하도록 하겠습니다.

Mixture Model
쌍봉 낙타의 등 같은 히스토그램이 있을 때, 이러한 분포에 대해서 단일 정규 분포로 표현하는 것은 무리가 있습니다. 즉, 설명력이 떨어질 수 있습니다. 이러한 경우, 2개 이상의 정규 분포가 혼합(mix)되어 있는 형태라고 표현하는 것을 Mixture model 이라고 합니다.

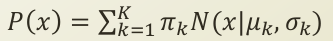
위의 식들의 term들을 살펴보면, 아래와 같습니다.
- π_k : 여러 정규분포들의 가중합에서 가중치를 나타냄.
- 0 <= π_k <= 1
- 확률(probability)의 형태
- 새로운 변수로써 Z라고 칭합니다.
-
N(x μ_k , σ_k) : k번째 정규 분포(subpopulation이라 칭함)의 pdf함수
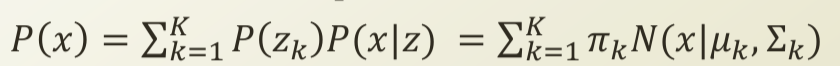
위에서 확률값의 형태를 지니는 새로운 변수 π_k 의 형태를 조금 변형해, P(z_k)로 하자고 했으므로, 위와 같은 등식이 성립됩니다. z_k에 따라서, 다수의 정규 분포들이 혼합되게 되는 것이죠. Mixing coefficient 또는 Selection variable 이라고 부릅니다.
z_k 의 특징에 대해, 다시 짚고 넘어가 보면, 각각은 확률값을 띄고, {0,1}의 확률 변수값만 지닙니다. 예로 들어서, P(z_k = 1 ) = π_k 이다. 와 같은 것이죠. 즉, π_k는 확률값 그 자체이고, z_k 은 확률 변수 값이 됩니다. 만약 k가 3이면,
P(z_1 = 1 ) = π_1
P(z_2 = 1 ) = π_2
P(z_3 = 1 ) = π_3
P(Z) = π_1*(1-π_1)*π_2*(1-π_2)*π_3*(1-π_3)
Multinomial distribution의 형태가 된다.
나머지 term(normal distribution pdf function)은 그대로 곱셈 연산이 적용됩니다.


바로 위에 나오는 이미지는 marginalized probability라고 불리는 부분입니다. 즉, 위에서 π_k와 같은 확률값 그 자체를 z_k라는 확률 변수 형태로 바뀌줌으로써, P(z_k)를 풀어나가면서, multinomial distribution이라는 결론에 도달하였는데, 이번에는 데이터(observations)라는 sub_term을 추가해 z_nk로 만들어주고 rho function를 씌워줌으로써, x_n 라는 데이터가 k번째 mixture distribution에 속할 확률 이라는 개념을 만들어냈습니다. 우변의 분모는 marginalize out 시켜주기 위해서 모든 k의 경우를 더한 것이고, 분자는 k의 경우만 나타낸 것이 되겠습니다.
맨 처음에 K-Means Algorithm을 다루다가 갑자기 왜 Gaussian Mixture Model 이 나오고, 거기에 더해서 복잡한 식들과 합께, 특정 데이터가 특정 mixture distribution에 속할 확률을 알아야 할까요?! 그 이유는 바로 GMM 와 K-Means 알고리즘 사이의 유사성에 기인합니다.
- 두 알고리즘 모두 두 개의 상호작용하는 파라미터들을 가지고 있습니다.
- K-Means 의 경우 할당 계수(r_nk) 와 센트로이드(Mu_k)
- GMM 의 경우, normal distribution의 parameter 와, 가중치 계수
- EM(Expectation - Maximization) 방법을 사용해서 최적화합니다.
- Expectation : 클러스터들과 데이터 점들 사이의
할당 - Maximization : 파라미터
업데이트
- Expectation : 클러스터들과 데이터 점들 사이의
Expectation step

처음이면 arbitrary parameter x, π, μ, Σ 에 따라서,rho(z_nk)를 계산합니다. rho(z_nk)를 통해서, assignment probability를 계산할 수 있게 됩니다. 이에 따라서, 가장 가까운 클러스터에 데이터를 할당합니다. 이렇게 계산된 rho(z_nk)는 새로운 파라미터를 업데이터하는 데에 사용됩니다.
Maximization step

위의 식은 이전에 계산했던, multinomial distribution 의 최적화한 값과, Multivariate normal distribution 의 최적화한 값을 적용한 것에 따른 것입니다. 전체적인 계산 과정에 대한 별다른 언급은 생략하겠으나, 하나만 다뤄보면, 마지막 두 번째 줄의 우변에서, {} 내부 항의 첫 번째 항의 합(n=1 -> N)을 계산해보면, N * (1/K) 정확히 같지는 않겠지만, marginal out 되어 있는 상태입니다. 이 됩니다. 하지만, 이때 외부 항에 있는 합(k=1 -> K)을 대입하면, N * K * (1/K) = N이 됩니다. 이에 따라, Lagrange method 의 lambda 는 -N이라는 결론에 다다릅니다. 결과적으로 π_k의 optimal(updated)값을 알 수 있게 됩니다.
Relation between K-Means and GMM
GMM 와 K-Means 두 알고리즘 사이의 차이는 각각의 Mixture model의 distribution의 분산이 같은지 다른지에 대한 것입니다. 즉, GMM의 경우 존재하는, 공분산 행렬이 K-Means Algorithm에서는 모든 distribution 의 분산을 같다고 가정하면서, e * Identity matrix로 표현하게 되는 것입니다. 이에 따라서, EM 최적화 프로세스 과정이 구분됩니다.

Expectation - Maximization
K-Means Algorithm 에서 EM 방법이 쓰이는 이유는, 비지도 학습이기 때문임을 넘어서, interactive parameter를 가지고 있기 때문입니다. 즉, 하나의 파라미터가 변화함에 따라, 다른 파라미터가 영향을 받아 최적화 과정에서 그 움직임이 변화하며, 복수 개의 파라미터가 최적점을 찾아가는 과정(iterative process)에 EM 방법이 쓰이는 것이죠.
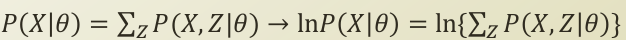
위의 식들을 순서대로, 나열해보면 다음과 같습니다.
-
P(X θ) = SUM_z(P(X,Z θ)) : latent variable Z 가 추가되면서, marginal out 시킴으로써 양변을 같게 만듭니다. -
ln(P(X θ)) = ln(SUM_z(P(X,Z θ))) : 양변에 자연로그를 씌워줍니다.
자연로그를 취해줌으로써, monotonous를 유지하면서, 미분을 편하게 하려 했지만, 내부 항에 있는 Summation으로 인해, 계산이 복잡해졌습니다. 이에 따라, E 과정 M 과정을 통해, 자체적으로 최적화를 실시합니다.
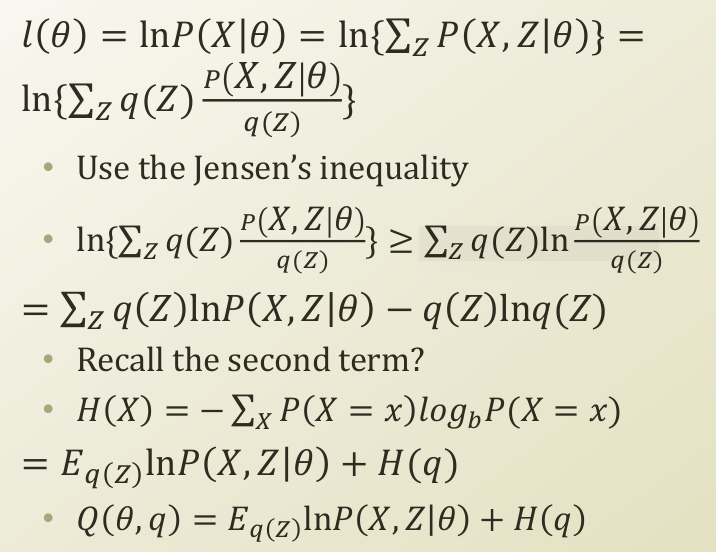
우리가 계산하려는, log likelihood 는 일단, log 함수입니다. log 함수는 concave 함수입니다.
Jensen’s inequality를 맞춰주기 위해서, q(Z) term을 의도적으로 추가해주고, 부등식을 만들어줍니다.
부등식이 성립하는 대신, SUM_z가 자연 로그 항에서 빠져나오게 되었습니다.
빠져나옴으로써, 계산이 편해진 우변을 계속해서 분해해보면, SUM_z(q(Z)ln(P(X,Z|θ) - q(Z)ln(q(Z)))) 항이 됩니다.
-q(Z)ln(q(Z)) 에서 q(Z)를 확률의 형태로 해석하면 entropy의 식과 같아집니다.
분해한 좌변의 머리부분에 E_q(Z)가 갑자기 씌워졌는데, q(Z)를 확률의 형태로 해석하면서, 가중 평균(weighted average)가 되면서 씌워진 것입니다. 이렇게 재해석한 분해값들의 합을 Q(θ|q)라고 부르도록 합니다.
| 중요한 부분을 놓칠 뻔 했는데요. 저희가 구한 Q(θ | q) 값은 실제 log likelihood의 lower bound 입니다. |
| 즉, 실제 값은 Q(θ | q)보다 크다는 것이죠. 이에 따라서, 실제 값과 근사하게 하기 위해서는 Q(θ | q)를 극대화(Maximizing)하면 됩니다. |

| 극대화를 위해, 식을 이리저리 재조립(rearrange)을 해봅니다. 위의 이미지의 마지막 식에서 유레카가 나옵니다! ln(P(X | θ)) - SUM_z{q(Z)ln(q(Z) / P(Z | X,θ))} 부분이 나오는데, 이 식의 좌변은 저희가 원래 구하려고 한, latent variable 이 있는 그 log likelihood입니다. 우변의 마이너스 term 으로 인해 inequality가 성립함을 알 수 있습니다. |

마지막 항을 딥러닝의 loss function으로 많이 사용되는 cross_entropy 와 긴밀히 연관된 kull-back leiber 입니다. 두 확률 분포의 유사성에 대한 지표로 사용되며, 유사할 수록 그 값은 0으로 작아집니다.

저희는 Q(θ,q)를 최대화시킴으로써, L(θ,q)를 최소화시킴으로써, 실제 값에 가까워질 수 있습니다. 하지만 Q(θ,q) 식에서, q(Z)에 대한 정보가 없습니다. 즉, L(θ,q)를 통해 알아내야 하는 것이죠. 이에 따라서, L(θ,q)를 최소화하는 최적화를 통해 q_t(z) 를 구하고, 그렇게 최적화된, q(z_t)를 Q(θ,q)에 집어 넣는 것이죠. 이번에는 업데이트된 q_t(z)를 통해, θ_t를 업데이트합니다. 그 후, 다시 L(θ,q)로 가서 새로운 q_{t+1}을 찾는 것이죠.
- L(θ,q)에서 q_t를 찾는다 -> Expectation step
- Q(θ,q)에서 θ_t를 찾는다 -> Maximiation step

위와 같은 EM looping 을 수렴할 때까지(KL가 0으로 수렴할 때까지) 실행하게 됩니다.
Comments