경사 하강법 (Gradient descent)
06 Jan 2019 | Machine_Learning HS
본 포스팅은 카이스트 문일철 교수님의 강좌와 위키피디아를 참조하였습니{}.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
Gradient Method
이전의 포스팅 Logistic Regression 에서 MLE를 통해 구한 모수 값이 비선형 방정식 형태로 인해 닫힌 해(closed form)이 나오지 않으면서 수치적 최적화 방법을 이용해서 최적에 가까운(approximation) 값을 구하는 방식을 택했습니다. 이번 포스팅은 수치적 최적화 방법 중 하나인 Gradient descent 방법에 대해서 이야기해보겠습니다.
강좌 노트에는 다음과 같이 작성되어 있는데요.
- Gradient descent/ascent method is
- Given a differentiable function of f(x) and an initial parameter of x_1
- Iteratively moving the parameter to the lower/higher value of f(x)
- By taking the direction of the negative/positive gradient of f(x)
해석해보면 아래와 같습니다.
- 초기값을 X_1으로 가지는 미분 가능 함수 f(x)에 따라, f(x)의 해당 점의 (초기값은 x_1) 미분값을 방향으로 삼아 f(x) 의 값을 위 아래로 계속 움직이는 것을 반복해 국지적 최소점(local minimum)을 찾는다.
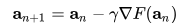
위의 함수에서 lambda 값은 learning rate 로 얼마만큼의 스텝(step)으로 움직일 것인지를 정하는 파라미터입니다.

사진에서 알 수 있다시피, gradient_descent 방식은 x_0에서 x_4로 갈 수록 그 값이 작아지는 특성을 가지고 있고,
F가 convex function 이면, 모든 국소 최소값은 전역 최소값을 의미하기 때문에, 경사 하강법은 전역 최소값에서 수렴(converge)함을 알 수 있습니다.
Stochastic gradient descent
위에서 다룬 gradient descent에서 stochastic 이라는 term 이 추가되었습니다. 어떻게 다를까요? 우선 stochastic 이란 확률적이라는 의미로, randomized sampling 의 경우 사용됩니다. 이러한 random sampling 기법을 사용한 gradient descent 를 의미하는 것이 바로 SGD 인데요. 왜 이 기법을 사용하는 것일까요?
gradient descent 는 해당 함수의 기울기에 step-size(머신 러닝에서는 learning rate이라 칭합니다.)을 곱한 만큼으로 이동해 새로운 파라미터로 업데이트 시켜줍니다.
근데 만약 저희가 가지고 있는 데이터가 google data라고 해봅시다. 그러면 데이터의 기울기를 계산해야 하는데, 엄청난 연산이 요구되겠죠? 이 때, 전체 데이터 중 일부만 stochastic 하게 추출해서 이들의 기울기만 계산해 업데이터 하는 것을 의미합니다.
여기서 단어가 하나 나오는데요. 바로 batch 입니다. batch란 트레이닝 샘플의 그룹을 의미하는 것으로, 기존의 Gradient descent 는 batch 가 전체 데이터 세트였다면 SGD에서는 배치가 stochastic 하게 추출된다는 것이죠(크기는 정할 수 있습니다).
역시나 SGD 방식에도 장단점이 존재하겠죠!!
장점은 빠른 업데이트 속도에 있으며, 단점은 local minimum 에 빠질 수 있다는 것입니다. 전체 데이터를 쑥 보고 움직이는 것이 아니라, 부분적 데이터만 보고 업데이트 되기 때문에, 그 다음에 어디로 갈지는 부분적 데이터에 의존하게 되고 만약 local minimum 이 있는 함수 형태였다면 그 속에 빠질 수 있다는 것이죠.
마지막으로 위키피디아에 기제된 경사 하강법의 한계(limitation)에 대해 언급하자면, 다른 방법보다 수렵의 점근도가 낮다고 합니다. 즉, 수렴의 속도가 늦다는 것이죠. 또한, 미분이 안되는 함수의 경우, gradient method 가 잘 작동하지 않는다고 합니다. 추가적인 description 이 있지만, 충분한 이해가 가지 않아 자세한 부분은 링크 의 Limitations 부분을 참고해주세요.
본 포스팅은 카이스트 문일철 교수님의 강좌와 위키피디아를 참조하였습니{}.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
Gradient Method
이전의 포스팅 Logistic Regression 에서 MLE를 통해 구한 모수 값이 비선형 방정식 형태로 인해 닫힌 해(closed form)이 나오지 않으면서 수치적 최적화 방법을 이용해서 최적에 가까운(approximation) 값을 구하는 방식을 택했습니다. 이번 포스팅은 수치적 최적화 방법 중 하나인 Gradient descent 방법에 대해서 이야기해보겠습니다.
강좌 노트에는 다음과 같이 작성되어 있는데요.
- Gradient descent/ascent method is
- Given a differentiable function of f(x) and an initial parameter of x_1
- Iteratively moving the parameter to the lower/higher value of f(x)
- By taking the direction of the negative/positive gradient of f(x)
해석해보면 아래와 같습니다.
- 초기값을 X_1으로 가지는 미분 가능 함수 f(x)에 따라, f(x)의 해당 점의 (초기값은 x_1) 미분값을 방향으로 삼아 f(x) 의 값을 위 아래로 계속 움직이는 것을 반복해 국지적 최소점(local minimum)을 찾는다.
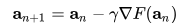
위의 함수에서 lambda 값은 learning rate 로 얼마만큼의 스텝(step)으로 움직일 것인지를 정하는 파라미터입니다.

사진에서 알 수 있다시피, gradient_descent 방식은 x_0에서 x_4로 갈 수록 그 값이 작아지는 특성을 가지고 있고,
F가 convex function 이면, 모든 국소 최소값은 전역 최소값을 의미하기 때문에, 경사 하강법은 전역 최소값에서 수렴(converge)함을 알 수 있습니다.
Stochastic gradient descent
위에서 다룬 gradient descent에서 stochastic 이라는 term 이 추가되었습니다. 어떻게 다를까요? 우선 stochastic 이란 확률적이라는 의미로, randomized sampling 의 경우 사용됩니다. 이러한 random sampling 기법을 사용한 gradient descent 를 의미하는 것이 바로 SGD 인데요. 왜 이 기법을 사용하는 것일까요?
gradient descent 는 해당 함수의 기울기에 step-size(머신 러닝에서는 learning rate이라 칭합니다.)을 곱한 만큼으로 이동해 새로운 파라미터로 업데이트 시켜줍니다.
근데 만약 저희가 가지고 있는 데이터가 google data라고 해봅시다. 그러면 데이터의 기울기를 계산해야 하는데, 엄청난 연산이 요구되겠죠? 이 때, 전체 데이터 중 일부만 stochastic 하게 추출해서 이들의 기울기만 계산해 업데이터 하는 것을 의미합니다.
여기서 단어가 하나 나오는데요. 바로 batch 입니다. batch란 트레이닝 샘플의 그룹을 의미하는 것으로, 기존의 Gradient descent 는 batch 가 전체 데이터 세트였다면 SGD에서는 배치가 stochastic 하게 추출된다는 것이죠(크기는 정할 수 있습니다).
역시나 SGD 방식에도 장단점이 존재하겠죠!!
장점은 빠른 업데이트 속도에 있으며, 단점은 local minimum 에 빠질 수 있다는 것입니다. 전체 데이터를 쑥 보고 움직이는 것이 아니라, 부분적 데이터만 보고 업데이트 되기 때문에, 그 다음에 어디로 갈지는 부분적 데이터에 의존하게 되고 만약 local minimum 이 있는 함수 형태였다면 그 속에 빠질 수 있다는 것이죠.
마지막으로 위키피디아에 기제된 경사 하강법의 한계(limitation)에 대해 언급하자면, 다른 방법보다 수렵의 점근도가 낮다고 합니다. 즉, 수렴의 속도가 늦다는 것이죠. 또한, 미분이 안되는 함수의 경우, gradient method 가 잘 작동하지 않는다고 합니다. 추가적인 description 이 있지만, 충분한 이해가 가지 않아 자세한 부분은 링크 의 Limitations 부분을 참고해주세요.
Comments