히든 마코프 모델, HMM
20 Feb 2019 | Machine_Learning HS
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
Hidden Markov Model
본격적으로 시작하기에 앞서, 강의에서 제시한 HMM 의 주요 세 가지 질문에 대해서 써놓고 넘어가도록 하겠습니다. 각각이 어떤 것을 의미하는 지는 진행하면서 계속해서 풀어보도록 하겠습니다.
- Evaluation question 풀기
- Decoding question 풀기
- Learning question 풀기
Time Series Data for GMM
저번 포스팅 에서 다뤘던, 가우시안 혼합 모형(GMM)에서 가우시안 정규 분포를 가지는 파라미터와 함께 잠재 변수를 가진 모델에 대해 EM 방법을 통해, 파라미터를 추정하는 과정에 대해서 이야기해보았습니다.
그러한, GMM 모형을 K-Means algorithm 과 비교하면서, 두개의 변수 즉, 2차원 공간에서 데이터들이 흩뿌려졌을 때, 이들을 어떻게 비지도 학습으로 클러스터(cluster)를 구성할 수 있는 지에 대해서 이야기해보았는데, 여기서 나온 2차원 공간(space,dimension)은 가역적(inversible)인 특징을 가지고 있습니다. 즉, 데이터들(observations)마다, 저마다의 자유로운 특성 즉, 공간을 지닐 수 있다는 것이죠.
하지만, 시간의 흐름(time-series)의 경우 이야기가 달라집니다. 시간은 한 번 흐르면 다시 되돌릴 수 없기 때문에, 기존에 적용했던, GMM 모형에 Time 이라는 Variable 이 들어가게 되면, 새로운 structure를 구성해야 하는 의무가 생기게 됩니다. 그렇게 나오는 모델이 바로 이번 포스팅에서 다룰 HMM , 히든 마코프 모델입니다.
HMM이 적용될 수 있는 예시를 강의에서 나온 몇 가지를 가지고 들어보겠습니다.
- 주식시장의 변동의 주기적 패턴을 잡는다.
- 상승장 -> 하락장 -> 보합장 : 각 기간의 특성이 존재할 것이다.
- 문장을 쪼개면 단어들의 시퀀스가 생기는데, 단어들의 시퀀스의 패턴을 잡는다.
- 주어에 “나” 이라는 단어가 나오면 “는” 이라는 단어가 나올 확률
위의 이미지에서 왼쪽 부분이 저번 포스팅에서 다룬 GMM이고, 오른쪽 부분이 GMM에서 Time-series 의 성질을 가미한 HMM 이 되겠습니다. 각각의 term들을 살펴보겠습니다.
- π : 잠재변수 z를 결정하는 파라미터
- z_k : 혼합모형(mixture model)에서 각각의 분포 k개를 선택하게 될 잠재 변수
- 확률 분포의 특징으로 continuous , discrete의 특성을 가질 수 있습니다.
- 이번 포스팅에서는 discrete 한 경우만, 다룹니다. 잠재 변수가 continous 한 경우, 이를 Kalman filter라 부릅니다.
- x_k : 잠재변수에 따라 선택되는 확률 분포 (GMM에서는 Gaussian Normal distribution)
- 확률 분포의 특징으로 continuous , discrete의 특성을 가질 수 있습니다.
중점을 두어야 하는 부분은, 잠재 변수 간의 독립성입니다. GMM의 경우 각각의 잠재 변수가 독립 성을 유지하지만, HMM의 경우, 시간이 지남에 따라, 이전 기간 t-1 시점의 변수가 t 시점에 영향을 미치기 때문에, 관계성을 가지게 되는 것입니다. 이에 따라, 잠재 변수 뿐만 아니라, 확률 분포 간에도 관계성이 생기게 됩니다.
HMM의 3 가지 Probability
- Initial State probability
- P(z_1) = Mult(π_1,..,π_k)
- 이전에 잠재 변수 z를 discrete 한 확률 변수로 가정하였기 때문에, 파라미터가 k개인 multinomial distribution이 됩니다.
- Transition probabilities
-
P(z_t
z_{t-1}i = 1) ~ Mult(a{i,1},a_{i,2},..,a_{i,k})
- t-1 시점에서는 i 클러스터에 있었을 때, t 시점에 각각의 클러스터에 속할 확률을 의미합니다.
- Initial state probability 와 구분되어야 하기 때문에, π -> z_1 의 관계를 제외한 z -> z 의 관계에서의 확률이 되겠습니다.
-
P(z_t_j = 1
z_{t-1}i = 1) = a{i,j}
- 일반화하면 위와 같습니다.
- Emission probabilities
-
P(x_t
z_t_i = 1) ~ Mult(b_{i,1} ,…, b_{i,m}) ~ f(x_t
θ_i)
- 특정 클래스의 잠재 변수가 주어졌을 때, 동일 시점에서 각각의 클러스터에 해당하는 확률 분포가 등장할 확률입니다.
-
P(z_t_j = 1
x_{t-1}i = 1) = b{i,j}
- 일반화하면 위와 같습니다.
- 정리하자면, 제일 처음 정해진 잠재변수에 대한 파라미터 π에 의해 나오는 잠재변수 출현에 대한 확률을 Initial state probability 라 하고, 시점이 이동하면서 잠재변수가 또 다른 잠재변수를 출현시키는 데 이에 따른 확률을 Transition probability 라 하며, 마지막으로 동일 시점에서 특정 잠재변수가 어떠한 확률 분포를 낳는 확률을 Emission probability라고 합니다. 각각의 용어의 뜻을 헤아려보면 맥락이 맞습니다.
Main Questions on HMM
제일 위에서 언급했었던 HMM의 세 가지 주요 문제들에 대해서 이야기해보려 합니다.
- Evaluation question :
- π , a , b , X 가 주어진 상황에서,
-
P(X
M,π,a,b)를 구하는 문제. (M 은 HMM의 structure를 의미합니다.)
- 즉, 이미 다 트레이닝을 시킨 상태에서, 우리가 만든 모델이 얼마나 그럴듯하냐(likely)의 문제입니다. 말 그대로 평가인 셈이죠.
- Decoding question :
- π , a , b , X 가 주어진 상황에서,
-
argmax_z(P(Z
X,M,π,a,b))를 구한다. 즉, Z를 구하는 문제
- 가장 괜찮은(probable) 잠재변수 Z를 구하는 문제입니다.
- 우리가 가질 수 있는 데이터와 파라미터를 다 가진 상태에서 구하려고 하는 값만 남았으니, supervised learning의 형태가 됩니다.
- Learning question :
- X 가 주어진 상황에서,
-
argmax_{π,a,b}(P(X
M,π,a,b))를 구하는 문제. 즉, 파라미터를 구하는 문제
- 모든 머신러닝 문제가 그러하듯, 최적의 파라미터를 구하는 과정이 되겠습니다.
- 우리가 가지고 있는 파라미터가 없는 상태에서 그 파라미터를 구하려는 문제이니, unsupervised learning이 되겠습니다.
이제 느낌이 오실 지 모르겠습니다. 저희는 결국 supervised learning인, Decoding question에 대한 답을 내기 위해서, π,a,b,M에 대해 알아야 하고, 이에 따라 Learning question에 대한 답을 내야 합니다. 이 반대도 마찬가지가 됩니다. 즉, HMM 프로세스도 EM 방법을 따르게 됩니다.
Obtaining π, a, b given X and M
강의에서 나온 예시를 들어서 문제를 한 번 풀어보도록 하겠습니다.
- 딜러가 주사위를 던지는 데, 사실은 주사위의 종류가 두 가지가 있습니다.
- fair dice : 모든 경우의 수가 1/6 로 동일하다.
- loaded dice : 6이 나올 확률은 1/2, 나머지는 1/10 로 un-fair 하다.
- 딜러는 주사위를 한 번만 던지는 것이 아닌, 여러 번 던진다.
- loaded dice 를 던지고 다시 한 번 더 loaded dice 를 던질 확률은 0.7
- fair dice 를 던지고 다음 번에는 loaded dice 를 던질 확률은 0.5
- dice의 선택에 대한 것은 binary이니, 각각의 상황에 대한 확률이 모두 할당됩니다.
그렇다면 이제 joint probability 를 구해봅시다.
- P(166,LLL) : 세 번 모두 loaded dice 를 던져서 166이 나올 확률
- 1/2 X 1/10 X 7/10 X 1/2 X 7/10 X 1/2 = 0.0061 이 됩니다.
3번의 time-series sequence LLL 에 따른,경우의 수는 2의 3승으로 8이 됩니다. 즉, 지수적으로 joint probability의 combination이 증가함을 의미합니다.
하지만 저희는 K-Means clustering과 같이, 각각 클러스터에 속하는 분포만 알고 싶습니다. 즉, 정해진 파라미터에 따른 X만 알고 싶기 때문에, 위에서 나온 LLL과 같은 잠재 변수는 원하지 않는 것이죠. 이러한 경우에는 marginalize out 시켜주면 됩니다. 즉, joint probability에서 잠재변수에 대해 모두 summation을 취해주면 되는 것이죠.
위의 이미지와 같이 marginalize out시켜주게 되는데, 두번째 줄을 보면, joint probability가 a와 b의 두 term의 곱으로 나뉘어지게 됩니다. 즉, transition prob 와 emission prob의 곱이 되는데, 이는, joint probability에 대해 factorization을 통해서, 분해한 결과가 되겠습니다.
이렇게 분해한 값에 대해서, bayes topolgy를 적용하여서, 불필요한 연산을 줄일 수 있게 되는데요. Bayes ball 에 따라서, conditional independence 를 만족하는 부분들을 제거해줌으로써 가능합니다.
- 등식의 첫 번째 줄은 joint probability를 factorize한 결과입니다.
- 등식의 두 번째 줄은 coditional independence 를 만족하는 term들을 제거한 결과입니다.
- 등식의 세 번째 줄은 z에 대한 summation에 대해 무관한 값들을 앞으로 튀어나오게 한 결과입니다.
-
등식의 네 번째 줄은 이전에 정의한 transition prob 과 emission prob 으로 term들을 고쳐쓴 것입니다.
- 이렇게 해서 나온 마지막 등식이 의미하는 바는 아래와 같습니다.
- joint probability alpha_t_k 를 한 시점 전의 joint probability alph_{t-1}_i 과 transition prob을 곱하고, emission prob을 계수로 곱한 값으로써, 재귀적(recursive)으로 다음 시점의 joint probability를 정의한 것이 되겠습니다.
Dynamic Programming
머신러닝은 결국 프로그래밍화시켜야 하는 문제이기에, 해당 강의에 recursion 에 대한 알고리즘이 포함되어 있는 것 같습니다.
흔히 프로그래밍을 하면 다뤄보게되는, 피보나치 수열은 재귀적 프로그래밍의 대표 주자입니다. 이를 두 가지 방식으로 할 수 있는데 첫 번째 방식은 우리가 흔히 하는 하향식 방식입니다. 완전 탐색 알고리즘을 사용하는 것으로, 복잡한 문제를 나눠서 푸는 것입니다. fibo(n)을 fibo(n-1)과 fibo(n-2)로 나눠서 Decision Tree처럼 계속 divide해서 conquer하는 방식이죠. 답을 잘 풀 수는 있지만, 전부 해체시켜서 푸는 방식이기 때문에, 시간도 오래걸리고, 아래와 같은 방식은 함수의 결과값들을 메모리 위의 스택에 올려야 하기 때문에, 부하도 있게 됩니다. 시간 복잡도는 Big-O 표기법으로는 O(2^n)입니다.
def fibo(n):
if n==0:
return 0
elif n==1:
return 1
else :
return fibo(n-1) + fibo(n-2)
%time print(fibo(20))
Wall time: 3.8 ms
두 번째 방식은 동적 프로그래밍(Dynamic programming)을 사용한 것으로 10번째 피보나치를 가정할 때, 첫 번째 수열부터 하나씩 해결하는 상향식 방식입니다. 완전 탐색 알고리즘에서 사용한 스택 대신, 아래에서 사용한 FIBO 리스트처럼, 이전의 결과값을 기억해주는 Memoization table이 있기 때문에, 스택을 쌓지 않아도, 재귀 문제를 풀 수 있게 됩니다. 시간 복잡도는 Big-O 표기법으로는 O(n)입니다.
FIBO=[]
FIBO.append(0)
FIBO.append(1)
for i in range(2,21):
FIBO.append(FIBO[i-1]+FIBO[i-2])
%time print(FIBO[20])
Wall time: 716 µs
Forward Probability Caculation
다시 본론으로 돌아와서 이전에 구했던 joint probability에 대해서 자세히 살펴보도록 하겠습니다.
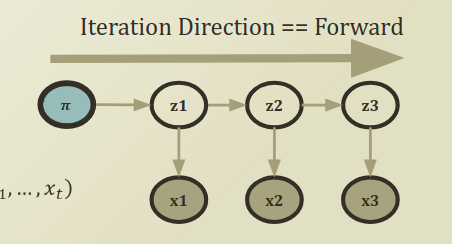
위의 이미지와 같이, Forward Algorithm은 시간이 지나감에 따라, 변화하는 joint probability 를 계산하는 것입니다. 이전에 이미 recursive 한 형태로 만들어주었기 때문에, iteration을 돌리면서 업데이트해가면 됩니다. 업데이트를 한다는 것은 미래 시점으로 이동해나간다 라고 할 수 있습니다.
다시 한번 더 짚고 넘어가기 위해, 위의 등식을 첨부하였는데, 앞의 marginalize out 시키는 시그마 term을 추가시켜줌으로써, 잠재변수 term을 제거하게 되어, 오직 x만 가지고 evaluation question 에 답을 할 수 있게 됩니다. 즉, P(X
Z,θ) -> P(X
θ)가 되는 것이죠.
안타깝게도 아직 끝난 것이 아닙니다. 지금까지 저희가 알게 된 것은, 위의 그래프로 예시를 들면, z_2가 특정 클러스터를 선택할 확률과 x1,x2에 대한 결합 확률을 알게 된 것이죠. 결국 marginalize out 시켜줌으로써, x1,x2에 대한 결합 확률만 남게 되는 것까지 왔습니다.
근데, time sequence 를 다루는 상황에서, 미래 시점에 대한 어떠한 기대(expectation)이 현재 시점의 어떠한 state를 결정한다면, 미래 시점의 state 또한 현재 시점을 결정하는 요인으로 들어가야 하지 않을까요? 이에 따라 나오는 것이 backward probability caculation입니다.
Backward Probability Calculation
- Backward Probability Calculation에서는 x들이 모두 주었을 때, 특정 시점의 잠재변수의 값의 확률을 알아내는 과정에 대해 다루게 됩니다.
X가 의미하는 것이 바로, time-series의 최종 길이 T까지의 x_i 세트이기 때문에, 전체 시점에 대한 x라고 할 수 있습니다. 이와 같은 x에 따른 특정 시점 t와 특정 클러스터 k의 잠재변수의 확률을 구하는 문제가 됩니다.
저희는 이미 joint probability를 알고 있기 때문에, 이로부터 손쉽게 유도할 수 있습니다.
- 등식의 첫 번째 줄은, joint prob을 factorize한 결과입니다.
- 등식의 두 번째 줄은, conditional independence한 term들을 topology에 따라, 제거한 것입니다.
- 등식의 첫 번째 줄은, P()안에 z{t+1}을 넣어주고, marginalize out 시켜준 결과입니다.
- 등식의 두 번째 줄은, factorize한 결과입니다.
- 등식의 세 번째 줄은, conditional independence한 term들을 topology에 따라, 제거한 것입니다.
이렇게 해서, backward probability 또한, recursive하게 등식을 만들었습니다.
forward probability 와 backward probability를 곱하게 되면,
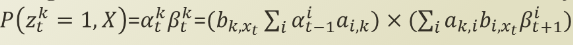
위의 이미지에서 X와 z에 대한 joint probability를 계산하기 위해서는, 구한 alpha와 beta가 필요하게 되고, 이렇게 구한 joint probability는 새로운 alpha ,beta 를 계산하는 데에 쓰이기 때문에, recursive 한 것이 되는 것이죠.
VITERBI DECODING
이름을 보면 아시다시피, 이번에는 Decoding problem 에 대해 해결하는 과정을 거쳐보겠습니다. 파라미터들을 찾아내기 위해, EM 방법을 사용한다고 말씀드렸는데, 지금까지 recursive 하게 forward probability , backward probability를 만들어내고, 이번엔 decoding 문제에 대해 다루는 이유는 결과적으로 learning question 을 해결하기 위한 작업이 되겠습니다. 즉, 토대가 되는 작업들입니다.
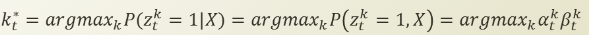
위의 등식은, 최적의 k를 찾는 공식입니다. 만약에, 주어진 observation X에 대해서, 가장 좋은 잠재변수를 알고싶다면, 어떻게 해야 할까요? 즉, P(z_t=1
X) 를 구하고 싶다면, 어떻게 해야 할까요? 이전에 이미 저희는 forward 와 backward 의 곱으로 joint probability를 구해놓았기 때문에, 이 또한 손쉽게 할 수 있습니다.
- V_t_k : forward approach 와 유사하지만, 이번에는 z 변수도 함께 들어가 있습니다. 이러한 joint prob을 maximize 하는 z 들을 t-1까지 구하는 것이 되겠습니다.
- 등식의 두 번째 줄은, factorize한 결과입니다.
- 등식의 세 번째 줄은, conditional independence한 term들을 topology에 따라, 제거한 것입니다.
- 등식의 네 번째 줄은, maximize 하게 하는 z들에 대해서 영향을 다르게 받는 term을 나눈 것입니다.
- 등식의 다섯 번째 줄은, 모델의 특성 상, t-1 시점의 잠재변수가 t시점의 잠재변수와 x에 끼칠 영향은 transition part 와 emission part의 곱으로 연결되어 있다는 것에 따른 결과입니다.
- 등식의 여섯 번째 줄은, transition 과 emission term들을 이전에 정의했던 term으로 바꾼 것입니다.
결국, X observation 에 따른, 잠재변수 z의 sequence 또한, recursive하게 정의되었습니다. 처음에 forward approach를 따랐기 때문에, 시간이 갈수록, 잠재변수 시점이 미래로 나아가게끔 되어있습니다.
Viterbi Decoding Algorithm
Viterbi decoding 에서 저희가 구하려고 하는 것은 probable latent variable의 “sequence” 입니다. 이에 따라서, 최적의 sequence 를 알아내기위한 알고리즘이 필요합니다.
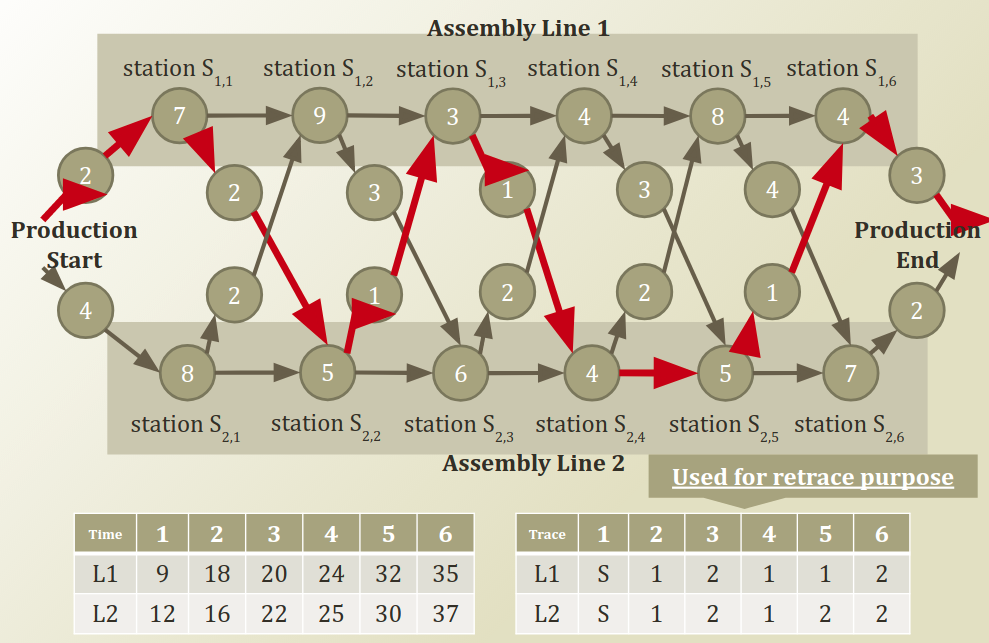
이번엔 강의 슬라이드 전체를 가지고 와봤는데요. start -> end 로 가는 전체 sequence 중 가장 optimal 한 sequence 를 찾는 문제입니다. 아래의 표를 보면, 왼쪽이 나아가는 approach를 기억해놓은 Memoization table 이고, 오른쪽이 retrace 하면서, 좀 더 시간이 적게 가는 쪽을 선택하게끔 하는 최적화과정을 의미합니다. 최단 거리가 나온 35를 어떤 sequence 를 거쳐야 가능한지를 retrace 과정을 통해서 추적하게 됩니다.
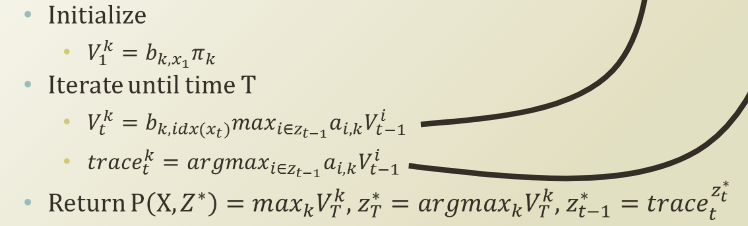
이제 이 알고리즘을 Decoding question에 적용을 해보겠습니다. Initilized 의 경우, transition problem 이 초기에는 intial state probability 가 되기 때문에, π 가 됩니다. T동안 iterate 를 하게 되면, forwarding 을 하면서 V_t_k 는 나아갑니다. 즉, memoization table 을 기반으로 recursion을 하게 되는 것이죠. 그와 동시에, 최적의 k 를 함께 계산하면서 optimal V_t_k를 위해선 어떤 sequence 를 따라야 하는 지를 retrace 하는 과정을 거치게 됩니다.
viterbi decoding 은 위와 같이 진행되지만, retrace 하면서, 최적화하는 과정에서 [0,1]의 값을 가지는 확률의 특성 상, 곱을 하게 되면, 0으로 수렴하게 되는 특징으로 vanishing 하는 문제가 발생할 수 있기 때문에, log domain 으로 전환해서 사용하게 됩니다.
EM for HMM
마지막 Learning question이 되겠습니다. 특정한 파라미터에 대해 알지 못하며 잠재 변수가 존재하는 상태에서, X만 가지고 파라미터들을 추정하는 과정은, GMM과 마찬가지고 EM 방법을 통해 해결할 수 있습니다.
수식도 너무 복잡하고, 전체 슬라이드를 가지고 오지 않고서는, 설명하는 것 뿐만 아니라 저자도 이해하기가 쉽지 않아, 전체를 가지고 왔습니다.
위의 슬라이드에서는 저희가 여기까지 오면서 해결했던 evaluation question 부분과 decoding question 부분이 등장하게 됩니다. 위에서 두 번째 등식 부분이 가장 likely한 X,Z를 만드는 파라미터들에 대해서, MLE에 따라서, 모두 곱을 하게 됩니다. 남은 term은 viterbi decoding 부분인데, 이부분에 대해서는 후에 EM 부분으로 미뤄두고, 우선 파라미터 최적화를 위해, 편미분을 취해 준 값을 도출하면 가장 아래 단계의 식이 나옵니다.
EM 방법을 HMM에서 사용하면 Baum Welch Algorithm이라고 합니다. 저희가 여태까지 했던 question을 사용해보면, Initilized paramter 로 viberti encoding을 해서, 최적의 z sequence 를 찾고(expectation), 이를 통해, parameter들을 optimize 하게 됩니다(Maximiation). 이를 iterate 하여 converge point 를 찾으면 되겠습니다.
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
Hidden Markov Model
본격적으로 시작하기에 앞서, 강의에서 제시한 HMM 의 주요 세 가지 질문에 대해서 써놓고 넘어가도록 하겠습니다. 각각이 어떤 것을 의미하는 지는 진행하면서 계속해서 풀어보도록 하겠습니다.
- Evaluation question 풀기
- Decoding question 풀기
- Learning question 풀기
Time Series Data for GMM
저번 포스팅 에서 다뤘던, 가우시안 혼합 모형(GMM)에서 가우시안 정규 분포를 가지는 파라미터와 함께 잠재 변수를 가진 모델에 대해 EM 방법을 통해, 파라미터를 추정하는 과정에 대해서 이야기해보았습니다.
그러한, GMM 모형을 K-Means algorithm 과 비교하면서, 두개의 변수 즉, 2차원 공간에서 데이터들이 흩뿌려졌을 때, 이들을 어떻게 비지도 학습으로 클러스터(cluster)를 구성할 수 있는 지에 대해서 이야기해보았는데, 여기서 나온 2차원 공간(space,dimension)은 가역적(inversible)인 특징을 가지고 있습니다. 즉, 데이터들(observations)마다, 저마다의 자유로운 특성 즉, 공간을 지닐 수 있다는 것이죠.
하지만, 시간의 흐름(time-series)의 경우 이야기가 달라집니다. 시간은 한 번 흐르면 다시 되돌릴 수 없기 때문에, 기존에 적용했던, GMM 모형에 Time 이라는 Variable 이 들어가게 되면, 새로운 structure를 구성해야 하는 의무가 생기게 됩니다. 그렇게 나오는 모델이 바로 이번 포스팅에서 다룰 HMM , 히든 마코프 모델입니다.
HMM이 적용될 수 있는 예시를 강의에서 나온 몇 가지를 가지고 들어보겠습니다.
- 주식시장의 변동의 주기적 패턴을 잡는다.
- 상승장 -> 하락장 -> 보합장 : 각 기간의 특성이 존재할 것이다.
- 문장을 쪼개면 단어들의 시퀀스가 생기는데, 단어들의 시퀀스의 패턴을 잡는다.
- 주어에 “나” 이라는 단어가 나오면 “는” 이라는 단어가 나올 확률
위의 이미지에서 왼쪽 부분이 저번 포스팅에서 다룬 GMM이고, 오른쪽 부분이 GMM에서 Time-series 의 성질을 가미한 HMM 이 되겠습니다. 각각의 term들을 살펴보겠습니다.
- π : 잠재변수 z를 결정하는 파라미터
- z_k : 혼합모형(mixture model)에서 각각의 분포 k개를 선택하게 될 잠재 변수
- 확률 분포의 특징으로 continuous , discrete의 특성을 가질 수 있습니다.
- 이번 포스팅에서는 discrete 한 경우만, 다룹니다. 잠재 변수가 continous 한 경우, 이를 Kalman filter라 부릅니다.
- x_k : 잠재변수에 따라 선택되는 확률 분포 (GMM에서는 Gaussian Normal distribution)
- 확률 분포의 특징으로 continuous , discrete의 특성을 가질 수 있습니다.
중점을 두어야 하는 부분은, 잠재 변수 간의 독립성입니다. GMM의 경우 각각의 잠재 변수가 독립 성을 유지하지만, HMM의 경우, 시간이 지남에 따라, 이전 기간 t-1 시점의 변수가 t 시점에 영향을 미치기 때문에, 관계성을 가지게 되는 것입니다. 이에 따라, 잠재 변수 뿐만 아니라, 확률 분포 간에도 관계성이 생기게 됩니다.
HMM의 3 가지 Probability
- Initial State probability
- P(z_1) = Mult(π_1,..,π_k)
- 이전에 잠재 변수 z를 discrete 한 확률 변수로 가정하였기 때문에, 파라미터가 k개인 multinomial distribution이 됩니다.
- Transition probabilities
-
P(z_t z_{t-1}i = 1) ~ Mult(a{i,1},a_{i,2},..,a_{i,k}) - t-1 시점에서는 i 클러스터에 있었을 때, t 시점에 각각의 클러스터에 속할 확률을 의미합니다.
- Initial state probability 와 구분되어야 하기 때문에, π -> z_1 의 관계를 제외한 z -> z 의 관계에서의 확률이 되겠습니다.
-
P(z_t_j = 1 z_{t-1}i = 1) = a{i,j} - 일반화하면 위와 같습니다.
-
- Emission probabilities
-
P(x_t z_t_i = 1) ~ Mult(b_{i,1} ,…, b_{i,m}) ~ f(x_t θ_i) - 특정 클래스의 잠재 변수가 주어졌을 때, 동일 시점에서 각각의 클러스터에 해당하는 확률 분포가 등장할 확률입니다.
-
P(z_t_j = 1 x_{t-1}i = 1) = b{i,j} - 일반화하면 위와 같습니다.
-
- 정리하자면, 제일 처음 정해진 잠재변수에 대한 파라미터 π에 의해 나오는 잠재변수 출현에 대한 확률을 Initial state probability 라 하고, 시점이 이동하면서 잠재변수가 또 다른 잠재변수를 출현시키는 데 이에 따른 확률을 Transition probability 라 하며, 마지막으로 동일 시점에서 특정 잠재변수가 어떠한 확률 분포를 낳는 확률을 Emission probability라고 합니다. 각각의 용어의 뜻을 헤아려보면 맥락이 맞습니다.
Main Questions on HMM
제일 위에서 언급했었던 HMM의 세 가지 주요 문제들에 대해서 이야기해보려 합니다.
- Evaluation question :
- π , a , b , X 가 주어진 상황에서,
-
P(X M,π,a,b)를 구하는 문제. (M 은 HMM의 structure를 의미합니다.) - 즉, 이미 다 트레이닝을 시킨 상태에서, 우리가 만든 모델이 얼마나 그럴듯하냐(likely)의 문제입니다. 말 그대로 평가인 셈이죠.
- Decoding question :
- π , a , b , X 가 주어진 상황에서,
-
argmax_z(P(Z X,M,π,a,b))를 구한다. 즉, Z를 구하는 문제 - 가장 괜찮은(probable) 잠재변수 Z를 구하는 문제입니다.
- 우리가 가질 수 있는 데이터와 파라미터를 다 가진 상태에서 구하려고 하는 값만 남았으니, supervised learning의 형태가 됩니다.
- Learning question :
- X 가 주어진 상황에서,
-
argmax_{π,a,b}(P(X M,π,a,b))를 구하는 문제. 즉, 파라미터를 구하는 문제 - 모든 머신러닝 문제가 그러하듯, 최적의 파라미터를 구하는 과정이 되겠습니다.
- 우리가 가지고 있는 파라미터가 없는 상태에서 그 파라미터를 구하려는 문제이니, unsupervised learning이 되겠습니다.
이제 느낌이 오실 지 모르겠습니다. 저희는 결국 supervised learning인, Decoding question에 대한 답을 내기 위해서, π,a,b,M에 대해 알아야 하고, 이에 따라 Learning question에 대한 답을 내야 합니다. 이 반대도 마찬가지가 됩니다. 즉, HMM 프로세스도 EM 방법을 따르게 됩니다.
Obtaining π, a, b given X and M
강의에서 나온 예시를 들어서 문제를 한 번 풀어보도록 하겠습니다.
- 딜러가 주사위를 던지는 데, 사실은 주사위의 종류가 두 가지가 있습니다.
- fair dice : 모든 경우의 수가 1/6 로 동일하다.
- loaded dice : 6이 나올 확률은 1/2, 나머지는 1/10 로 un-fair 하다.
- 딜러는 주사위를 한 번만 던지는 것이 아닌, 여러 번 던진다.
- loaded dice 를 던지고 다시 한 번 더 loaded dice 를 던질 확률은 0.7
- fair dice 를 던지고 다음 번에는 loaded dice 를 던질 확률은 0.5
- dice의 선택에 대한 것은 binary이니, 각각의 상황에 대한 확률이 모두 할당됩니다.
그렇다면 이제 joint probability 를 구해봅시다.
- P(166,LLL) : 세 번 모두 loaded dice 를 던져서 166이 나올 확률
- 1/2 X 1/10 X 7/10 X 1/2 X 7/10 X 1/2 = 0.0061 이 됩니다.
3번의 time-series sequence LLL 에 따른,경우의 수는 2의 3승으로 8이 됩니다. 즉, 지수적으로 joint probability의 combination이 증가함을 의미합니다.
하지만 저희는 K-Means clustering과 같이, 각각 클러스터에 속하는 분포만 알고 싶습니다. 즉, 정해진 파라미터에 따른 X만 알고 싶기 때문에, 위에서 나온 LLL과 같은 잠재 변수는 원하지 않는 것이죠. 이러한 경우에는 marginalize out 시켜주면 됩니다. 즉, joint probability에서 잠재변수에 대해 모두 summation을 취해주면 되는 것이죠.
위의 이미지와 같이 marginalize out시켜주게 되는데, 두번째 줄을 보면, joint probability가 a와 b의 두 term의 곱으로 나뉘어지게 됩니다. 즉, transition prob 와 emission prob의 곱이 되는데, 이는, joint probability에 대해 factorization을 통해서, 분해한 결과가 되겠습니다.
이렇게 분해한 값에 대해서, bayes topolgy를 적용하여서, 불필요한 연산을 줄일 수 있게 되는데요. Bayes ball 에 따라서, conditional independence 를 만족하는 부분들을 제거해줌으로써 가능합니다.
- 등식의 첫 번째 줄은 joint probability를 factorize한 결과입니다.
- 등식의 두 번째 줄은 coditional independence 를 만족하는 term들을 제거한 결과입니다.
- 등식의 세 번째 줄은 z에 대한 summation에 대해 무관한 값들을 앞으로 튀어나오게 한 결과입니다.
-
등식의 네 번째 줄은 이전에 정의한 transition prob 과 emission prob 으로 term들을 고쳐쓴 것입니다.
- 이렇게 해서 나온 마지막 등식이 의미하는 바는 아래와 같습니다.
- joint probability alpha_t_k 를 한 시점 전의 joint probability alph_{t-1}_i 과 transition prob을 곱하고, emission prob을 계수로 곱한 값으로써, 재귀적(recursive)으로 다음 시점의 joint probability를 정의한 것이 되겠습니다.
Dynamic Programming
머신러닝은 결국 프로그래밍화시켜야 하는 문제이기에, 해당 강의에 recursion 에 대한 알고리즘이 포함되어 있는 것 같습니다.
흔히 프로그래밍을 하면 다뤄보게되는, 피보나치 수열은 재귀적 프로그래밍의 대표 주자입니다. 이를 두 가지 방식으로 할 수 있는데 첫 번째 방식은 우리가 흔히 하는 하향식 방식입니다. 완전 탐색 알고리즘을 사용하는 것으로, 복잡한 문제를 나눠서 푸는 것입니다. fibo(n)을 fibo(n-1)과 fibo(n-2)로 나눠서 Decision Tree처럼 계속 divide해서 conquer하는 방식이죠. 답을 잘 풀 수는 있지만, 전부 해체시켜서 푸는 방식이기 때문에, 시간도 오래걸리고, 아래와 같은 방식은 함수의 결과값들을 메모리 위의 스택에 올려야 하기 때문에, 부하도 있게 됩니다. 시간 복잡도는 Big-O 표기법으로는 O(2^n)입니다.
def fibo(n):
if n==0:
return 0
elif n==1:
return 1
else :
return fibo(n-1) + fibo(n-2)
%time print(fibo(20))
Wall time: 3.8 ms
두 번째 방식은 동적 프로그래밍(Dynamic programming)을 사용한 것으로 10번째 피보나치를 가정할 때, 첫 번째 수열부터 하나씩 해결하는 상향식 방식입니다. 완전 탐색 알고리즘에서 사용한 스택 대신, 아래에서 사용한 FIBO 리스트처럼, 이전의 결과값을 기억해주는 Memoization table이 있기 때문에, 스택을 쌓지 않아도, 재귀 문제를 풀 수 있게 됩니다. 시간 복잡도는 Big-O 표기법으로는 O(n)입니다.
FIBO=[]
FIBO.append(0)
FIBO.append(1)
for i in range(2,21):
FIBO.append(FIBO[i-1]+FIBO[i-2])
%time print(FIBO[20])
Wall time: 716 µs
Forward Probability Caculation
다시 본론으로 돌아와서 이전에 구했던 joint probability에 대해서 자세히 살펴보도록 하겠습니다.
위의 이미지와 같이, Forward Algorithm은 시간이 지나감에 따라, 변화하는 joint probability 를 계산하는 것입니다. 이전에 이미 recursive 한 형태로 만들어주었기 때문에, iteration을 돌리면서 업데이트해가면 됩니다. 업데이트를 한다는 것은 미래 시점으로 이동해나간다 라고 할 수 있습니다.
| 다시 한번 더 짚고 넘어가기 위해, 위의 등식을 첨부하였는데, 앞의 marginalize out 시키는 시그마 term을 추가시켜줌으로써, 잠재변수 term을 제거하게 되어, 오직 x만 가지고 evaluation question 에 답을 할 수 있게 됩니다. 즉, P(X | Z,θ) -> P(X | θ)가 되는 것이죠. |
안타깝게도 아직 끝난 것이 아닙니다. 지금까지 저희가 알게 된 것은, 위의 그래프로 예시를 들면, z_2가 특정 클러스터를 선택할 확률과 x1,x2에 대한 결합 확률을 알게 된 것이죠. 결국 marginalize out 시켜줌으로써, x1,x2에 대한 결합 확률만 남게 되는 것까지 왔습니다.
근데, time sequence 를 다루는 상황에서, 미래 시점에 대한 어떠한 기대(expectation)이 현재 시점의 어떠한 state를 결정한다면, 미래 시점의 state 또한 현재 시점을 결정하는 요인으로 들어가야 하지 않을까요? 이에 따라 나오는 것이 backward probability caculation입니다.
Backward Probability Calculation
- Backward Probability Calculation에서는 x들이 모두 주었을 때, 특정 시점의 잠재변수의 값의 확률을 알아내는 과정에 대해 다루게 됩니다.
X가 의미하는 것이 바로, time-series의 최종 길이 T까지의 x_i 세트이기 때문에, 전체 시점에 대한 x라고 할 수 있습니다. 이와 같은 x에 따른 특정 시점 t와 특정 클러스터 k의 잠재변수의 확률을 구하는 문제가 됩니다.
저희는 이미 joint probability를 알고 있기 때문에, 이로부터 손쉽게 유도할 수 있습니다.
- 등식의 첫 번째 줄은, joint prob을 factorize한 결과입니다.
- 등식의 두 번째 줄은, conditional independence한 term들을 topology에 따라, 제거한 것입니다.
- 등식의 첫 번째 줄은, P()안에 z{t+1}을 넣어주고, marginalize out 시켜준 결과입니다.
- 등식의 두 번째 줄은, factorize한 결과입니다.
- 등식의 세 번째 줄은, conditional independence한 term들을 topology에 따라, 제거한 것입니다.
이렇게 해서, backward probability 또한, recursive하게 등식을 만들었습니다.
forward probability 와 backward probability를 곱하게 되면,
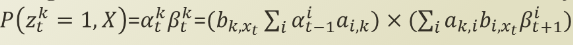
위의 이미지에서 X와 z에 대한 joint probability를 계산하기 위해서는, 구한 alpha와 beta가 필요하게 되고, 이렇게 구한 joint probability는 새로운 alpha ,beta 를 계산하는 데에 쓰이기 때문에, recursive 한 것이 되는 것이죠.
VITERBI DECODING
이름을 보면 아시다시피, 이번에는 Decoding problem 에 대해 해결하는 과정을 거쳐보겠습니다. 파라미터들을 찾아내기 위해, EM 방법을 사용한다고 말씀드렸는데, 지금까지 recursive 하게 forward probability , backward probability를 만들어내고, 이번엔 decoding 문제에 대해 다루는 이유는 결과적으로 learning question 을 해결하기 위한 작업이 되겠습니다. 즉, 토대가 되는 작업들입니다.
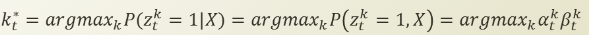
| 위의 등식은, 최적의 k를 찾는 공식입니다. 만약에, 주어진 observation X에 대해서, 가장 좋은 잠재변수를 알고싶다면, 어떻게 해야 할까요? 즉, P(z_t=1 | X) 를 구하고 싶다면, 어떻게 해야 할까요? 이전에 이미 저희는 forward 와 backward 의 곱으로 joint probability를 구해놓았기 때문에, 이 또한 손쉽게 할 수 있습니다. |
- V_t_k : forward approach 와 유사하지만, 이번에는 z 변수도 함께 들어가 있습니다. 이러한 joint prob을 maximize 하는 z 들을 t-1까지 구하는 것이 되겠습니다.
- 등식의 두 번째 줄은, factorize한 결과입니다.
- 등식의 세 번째 줄은, conditional independence한 term들을 topology에 따라, 제거한 것입니다.
- 등식의 네 번째 줄은, maximize 하게 하는 z들에 대해서 영향을 다르게 받는 term을 나눈 것입니다.
- 등식의 다섯 번째 줄은, 모델의 특성 상, t-1 시점의 잠재변수가 t시점의 잠재변수와 x에 끼칠 영향은 transition part 와 emission part의 곱으로 연결되어 있다는 것에 따른 결과입니다.
- 등식의 여섯 번째 줄은, transition 과 emission term들을 이전에 정의했던 term으로 바꾼 것입니다.
결국, X observation 에 따른, 잠재변수 z의 sequence 또한, recursive하게 정의되었습니다. 처음에 forward approach를 따랐기 때문에, 시간이 갈수록, 잠재변수 시점이 미래로 나아가게끔 되어있습니다.
Viterbi Decoding Algorithm
Viterbi decoding 에서 저희가 구하려고 하는 것은 probable latent variable의 “sequence” 입니다. 이에 따라서, 최적의 sequence 를 알아내기위한 알고리즘이 필요합니다.
이번엔 강의 슬라이드 전체를 가지고 와봤는데요. start -> end 로 가는 전체 sequence 중 가장 optimal 한 sequence 를 찾는 문제입니다. 아래의 표를 보면, 왼쪽이 나아가는 approach를 기억해놓은 Memoization table 이고, 오른쪽이 retrace 하면서, 좀 더 시간이 적게 가는 쪽을 선택하게끔 하는 최적화과정을 의미합니다. 최단 거리가 나온 35를 어떤 sequence 를 거쳐야 가능한지를 retrace 과정을 통해서 추적하게 됩니다.
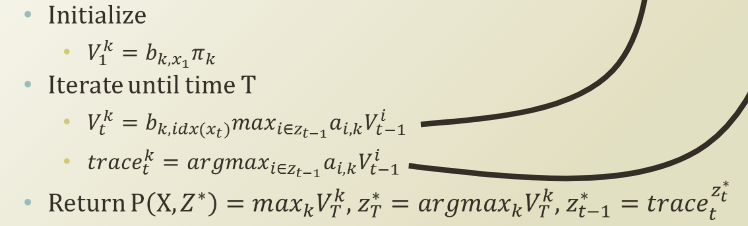
이제 이 알고리즘을 Decoding question에 적용을 해보겠습니다. Initilized 의 경우, transition problem 이 초기에는 intial state probability 가 되기 때문에, π 가 됩니다. T동안 iterate 를 하게 되면, forwarding 을 하면서 V_t_k 는 나아갑니다. 즉, memoization table 을 기반으로 recursion을 하게 되는 것이죠. 그와 동시에, 최적의 k 를 함께 계산하면서 optimal V_t_k를 위해선 어떤 sequence 를 따라야 하는 지를 retrace 하는 과정을 거치게 됩니다.
viterbi decoding 은 위와 같이 진행되지만, retrace 하면서, 최적화하는 과정에서 [0,1]의 값을 가지는 확률의 특성 상, 곱을 하게 되면, 0으로 수렴하게 되는 특징으로 vanishing 하는 문제가 발생할 수 있기 때문에, log domain 으로 전환해서 사용하게 됩니다.
EM for HMM
마지막 Learning question이 되겠습니다. 특정한 파라미터에 대해 알지 못하며 잠재 변수가 존재하는 상태에서, X만 가지고 파라미터들을 추정하는 과정은, GMM과 마찬가지고 EM 방법을 통해 해결할 수 있습니다.
수식도 너무 복잡하고, 전체 슬라이드를 가지고 오지 않고서는, 설명하는 것 뿐만 아니라 저자도 이해하기가 쉽지 않아, 전체를 가지고 왔습니다.
위의 슬라이드에서는 저희가 여기까지 오면서 해결했던 evaluation question 부분과 decoding question 부분이 등장하게 됩니다. 위에서 두 번째 등식 부분이 가장 likely한 X,Z를 만드는 파라미터들에 대해서, MLE에 따라서, 모두 곱을 하게 됩니다. 남은 term은 viterbi decoding 부분인데, 이부분에 대해서는 후에 EM 부분으로 미뤄두고, 우선 파라미터 최적화를 위해, 편미분을 취해 준 값을 도출하면 가장 아래 단계의 식이 나옵니다.
EM 방법을 HMM에서 사용하면 Baum Welch Algorithm이라고 합니다. 저희가 여태까지 했던 question을 사용해보면, Initilized paramter 로 viberti encoding을 해서, 최적의 z sequence 를 찾고(expectation), 이를 통해, parameter들을 optimize 하게 됩니다(Maximiation). 이를 iterate 하여 converge point 를 찾으면 되겠습니다.
Comments