로지스틱 회귀 (Logistic Regression)
06 Jan 2019 | Machine_Learning HS
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
로지스틱 회귀(Logistic Regression)
이전까지 나이브 베이즈 분류기 , 의사 결정 나무 로 두 가지 분류기에 대해서 이야기해보았는데 오늘 은 로지스틱 회귀에 따른 로지스틱 분류에 대해서 이야기해보겠습니다.
Linear Function vs. Non-Linear Function
- 선형의 회귀 분석이나 Decision boundary 가 선형일 경우의 문제가 무엇이 있을까요? 즉, 선형 함수에 대한 함수 트레이닝의 문제점은?
- 확률의 문제로 귀결시킬 때 문제가 됩니다. 0과 1 사이의 수가 나와야 하는데, 선형의 경우 계속해서 나아가기 때문이죠
- 1과 0의 분류 문제를 해결하는데 늦은 응답을 보입니다.
-
위와 같은 문제점을 개선하기 위해서, 확률의 공리(probability axiom)을 지키면서, 의사결정 경계 주변에서 빠른 응답을 보여주는 함수를 가져오는데 이를 바로 로지스틱 함수(logistic function)이라 합니다.
- 로지스틱 함수는 시그모이드 함수의 일종인데요. 시그모이드 함수의 특징은 아래와 같습니다.
- 경계가 존재
- 미분이 가능
- 실수로 정의가능한 함수
- 미분했을 때, 양수가 나오는 함수
이러한 특징을 가지고 있는 시그모이드 함수 중 하나인 로지스틱 함수는 아래와 같은 그래프로 시각화할 수 있습니다.
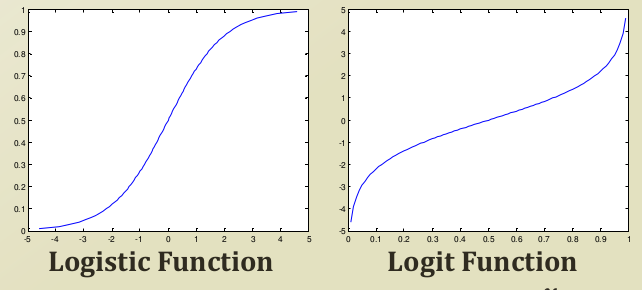
오른쪽 그래프는 Logit function 이라는 함수로 보시면 알 수 있다시피, logistic function의 inverse function입니다. 이를 같이 시각화하는 이유는, 각 함수에 따라 axis가 의미하는 것이 반대로 존재하기 때문에, 유도 과정에서 쓰이게 됩니다.

위의 이미지는 로지스틱 함수의 방정식입니다. 이러한 포맷을 가지게 된 이유는 y값이 [0,1] 의 형태를 지니게 하기 위함이고 x가 0일 때, 즉 sign이 바뀔 때, y값의 절반인 0.5의 값을 가지게 되기 때문입니다.
Logistic Function fitting
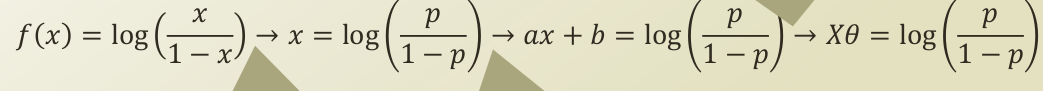
강의 자료를 그대로 캡쳐하는 바람에 이미지가 깔끔하진 못한데요. 식을 단계별로 해석해보겠습니다.
-
f(x) = log(x/(1-x)) : 해당 함수는 logistic function 의 역함수인 logit function의 식입니다.
-
-> x = log(p/(1-p)) : 여기서 -> x 라는 notation 이 나오는데요. [0,1] 의 범위값을 가지는 x를 확률의 도메인으로 가져와서, p로 notation을 바꾼 것이고, f(x)는 input feature의 값의 형태를 띄기 때문에, x로 notation을 바꾼 것입니다.
-
ax + b = log(p/(1-p)) : 2번의 x가 ax + b 로 바뀌었습니다. 이는 fitting 과정에서 발생하는 shift , drift 를 반영한 식이 되겠습니다. 즉, logistic function 이 딱 이쁘게 놓여져있는 것이 아닌, 데이터가 들어오면서 이리저리 옮겨가고 확장/축소된다는 것이죠.
-
Xθ = log(p(1-p)) : ax + b 를 Xθ 로 바꿨습니다. 이는 linear regression에서 쓰였던 bias augmentation 의 trick 으로써, X matrix 의 첫 번째 열 벡터를 1벡터로 추가시켜줌으로써, ax + b 의 상수항을 augmenting 시켜주는 것입니다.
선형 회귀를 제 블로그에서 아직 다루지는 않았지만, Xθ = P(Y
X) 라는 식으로 선형 회귀식을 최적화 fitting하게 됩니다. 즉, 데이터 X가 주어졌을 때, Y가 되는 값을 가장 잘 설명하는 선 Xθ(aw+b)을 만드는 것(근사하게) 이라는 것이죠.
하지만, 처음에 말씀드렸다시피 선형 회귀의 방식을 분류 문제에 적용하게 되면 확률의 공리를 지키지 못하게 됩니다.
이에 따라, logistic function을 적용하게 되었고, 선형 회귀에서 바뀌게 된 식은 아래와 같습니다.
-
Xθ = log(P(Y
X) / (1-P(Y
X)))
갑자기 이게 뭐지 하실 수 있지만, 4번까지 저희가 유도한 식에서 p 가 P(Y
X)로 바뀐 것입니다.

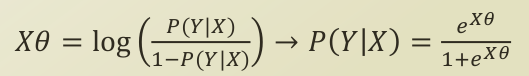
-> 기준으로 왼쪽의 식인 logit function이 inversing 되면서, logistic function이 됩니다. P(YX) 가 X라는 input data 가 들어갔을 때, Y라는 클래스에 들어갈 확률이 됩니다. 즉, 베이지안에 나오는 posterior probability가 되는데요. (베이지안 정리는 쓰지 않았으니, conditional probability라고 말하는게 맞겠네요.) 이 값이 커진다는 것은 분류가 잘 되고 있다는 것이니, 이를 최대화하는 최적화 문제가 됩니다. 이를 최적화하는 모수는 아시다시피, θ 가중치 벡터가 됩니다. 즉, P(Y
X)를 최대화시키는 θ 가중치 벡터 값을 찾는 문제가 됩니다.
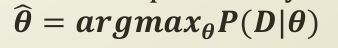
위의 등식은 위에서 길게 말씀드린 최적화 문제를 등식으로 표현한 것으로 Maximum Likelihood Estimation 문제로 귀결됩니다.
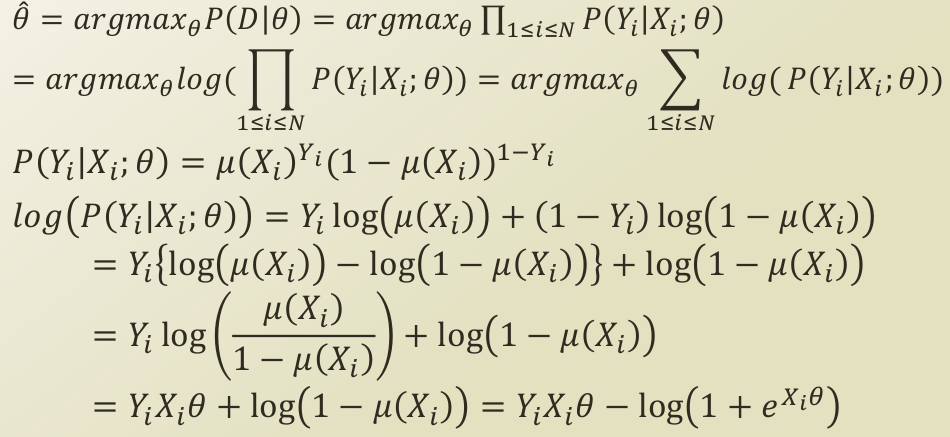
P(Y
X)를 최적화하기 때문에, 이를 θ로 미분하게 되는데, 로지스틱 회귀는 binary classification 이기 때문에, bernoulli distribution을 P(Y
X)로 두고 최적화를 진행합니다.
무엇보다 중요한 것은, 확률을 선형이 아닌, 확률의 공리를 충족하는 비선형 함수 logistic function을 가정하기 때문에, bernoulli distribution의 probability term에 logistic function을 대입해주어야 합니다.
최적화 과정은 김도형 박사님 블로그 가 개인적으로 이해하기 더 쉬워 이를 참고했는데요.

위에서 말씀드린 logistic_function을 확률값으로 대입해서 bernoulli distribution을 전개한 것입니다.
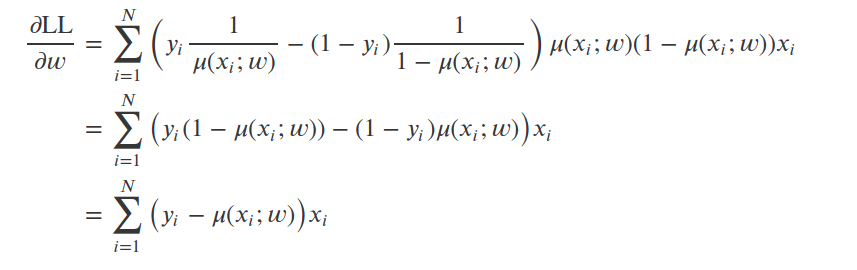
Log likelihood 를 미분의 chain rule 에 따라서 LL 에 대해 m(x_i;w) 로 미분해주고, m(x_i;w) 를 w로 미분하게 되어서 위와 같은 식이 나옵니다. 어떠한 w의 값이 딱 떨어져서 나오지 않네요. 이를 닫힌 값이 없다라고 합니다. 이에 따라 수치적 최적화(numerical optimization)을 통해 최적의 모수로 approximation 해야 합니다.
Numerical Optimization
저희는 LL 을 최대화했어야 했습니다. 근데 LL에 부호를 바꿔주게 되면 최소화시키는 최적화문제로 바뀌게 되었습니다. -LL을 w로 미분한 값에 learning rate이라는 hyper parameter 를 곱해주고 계속해서 w(모수)를 업데이트 시켜주면, 수치적 최적화 방법으로 최적 모수값을 구할 수 있게 됩니다. 이를 gradient descent 방법이라고 합니다. 보다 자세한 내용은 다음 포스팅에서 다루도록 하겠습니다.
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
로지스틱 회귀(Logistic Regression)
이전까지 나이브 베이즈 분류기 , 의사 결정 나무 로 두 가지 분류기에 대해서 이야기해보았는데 오늘 은 로지스틱 회귀에 따른 로지스틱 분류에 대해서 이야기해보겠습니다.
Linear Function vs. Non-Linear Function
- 선형의 회귀 분석이나 Decision boundary 가 선형일 경우의 문제가 무엇이 있을까요? 즉, 선형 함수에 대한 함수 트레이닝의 문제점은?
- 확률의 문제로 귀결시킬 때 문제가 됩니다. 0과 1 사이의 수가 나와야 하는데, 선형의 경우 계속해서 나아가기 때문이죠
- 1과 0의 분류 문제를 해결하는데 늦은 응답을 보입니다.
-
위와 같은 문제점을 개선하기 위해서, 확률의 공리(probability axiom)을 지키면서, 의사결정 경계 주변에서 빠른 응답을 보여주는 함수를 가져오는데 이를 바로 로지스틱 함수(logistic function)이라 합니다.
- 로지스틱 함수는 시그모이드 함수의 일종인데요. 시그모이드 함수의 특징은 아래와 같습니다.
- 경계가 존재
- 미분이 가능
- 실수로 정의가능한 함수
- 미분했을 때, 양수가 나오는 함수
이러한 특징을 가지고 있는 시그모이드 함수 중 하나인 로지스틱 함수는 아래와 같은 그래프로 시각화할 수 있습니다.

오른쪽 그래프는 Logit function 이라는 함수로 보시면 알 수 있다시피, logistic function의 inverse function입니다. 이를 같이 시각화하는 이유는, 각 함수에 따라 axis가 의미하는 것이 반대로 존재하기 때문에, 유도 과정에서 쓰이게 됩니다.

위의 이미지는 로지스틱 함수의 방정식입니다. 이러한 포맷을 가지게 된 이유는 y값이 [0,1] 의 형태를 지니게 하기 위함이고 x가 0일 때, 즉 sign이 바뀔 때, y값의 절반인 0.5의 값을 가지게 되기 때문입니다.
Logistic Function fitting
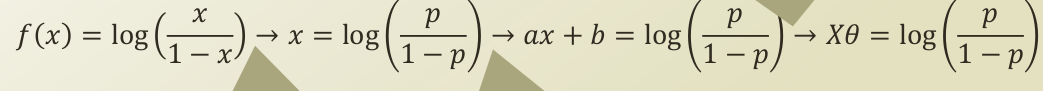
강의 자료를 그대로 캡쳐하는 바람에 이미지가 깔끔하진 못한데요. 식을 단계별로 해석해보겠습니다.
-
f(x) = log(x/(1-x)) : 해당 함수는 logistic function 의 역함수인 logit function의 식입니다.
-
-> x = log(p/(1-p)) : 여기서 -> x 라는 notation 이 나오는데요. [0,1] 의 범위값을 가지는 x를 확률의 도메인으로 가져와서, p로 notation을 바꾼 것이고, f(x)는 input feature의 값의 형태를 띄기 때문에, x로 notation을 바꾼 것입니다.
-
ax + b = log(p/(1-p)) : 2번의 x가 ax + b 로 바뀌었습니다. 이는 fitting 과정에서 발생하는 shift , drift 를 반영한 식이 되겠습니다. 즉, logistic function 이 딱 이쁘게 놓여져있는 것이 아닌, 데이터가 들어오면서 이리저리 옮겨가고 확장/축소된다는 것이죠.
-
Xθ = log(p(1-p)) : ax + b 를 Xθ 로 바꿨습니다. 이는 linear regression에서 쓰였던 bias augmentation 의 trick 으로써, X matrix 의 첫 번째 열 벡터를 1벡터로 추가시켜줌으로써, ax + b 의 상수항을 augmenting 시켜주는 것입니다.
| 선형 회귀를 제 블로그에서 아직 다루지는 않았지만, Xθ = P(Y | X) 라는 식으로 선형 회귀식을 최적화 fitting하게 됩니다. 즉, 데이터 X가 주어졌을 때, Y가 되는 값을 가장 잘 설명하는 선 Xθ(aw+b)을 만드는 것(근사하게) 이라는 것이죠. |
하지만, 처음에 말씀드렸다시피 선형 회귀의 방식을 분류 문제에 적용하게 되면 확률의 공리를 지키지 못하게 됩니다. 이에 따라, logistic function을 적용하게 되었고, 선형 회귀에서 바뀌게 된 식은 아래와 같습니다.
-
Xθ = log(P(Y X) / (1-P(Y X)))
| 갑자기 이게 뭐지 하실 수 있지만, 4번까지 저희가 유도한 식에서 p 가 P(Y | X)로 바뀐 것입니다. |

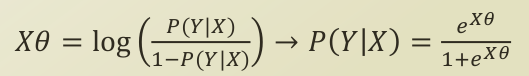
-> 기준으로 왼쪽의 식인 logit function이 inversing 되면서, logistic function이 됩니다. P(Y |
X) 가 X라는 input data 가 들어갔을 때, Y라는 클래스에 들어갈 확률이 됩니다. 즉, 베이지안에 나오는 posterior probability가 되는데요. (베이지안 정리는 쓰지 않았으니, conditional probability라고 말하는게 맞겠네요.) 이 값이 커진다는 것은 분류가 잘 되고 있다는 것이니, 이를 최대화하는 최적화 문제가 됩니다. 이를 최적화하는 모수는 아시다시피, θ 가중치 벡터가 됩니다. 즉, P(Y | X)를 최대화시키는 θ 가중치 벡터 값을 찾는 문제가 됩니다. |
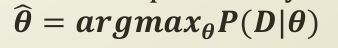
위의 등식은 위에서 길게 말씀드린 최적화 문제를 등식으로 표현한 것으로 Maximum Likelihood Estimation 문제로 귀결됩니다.
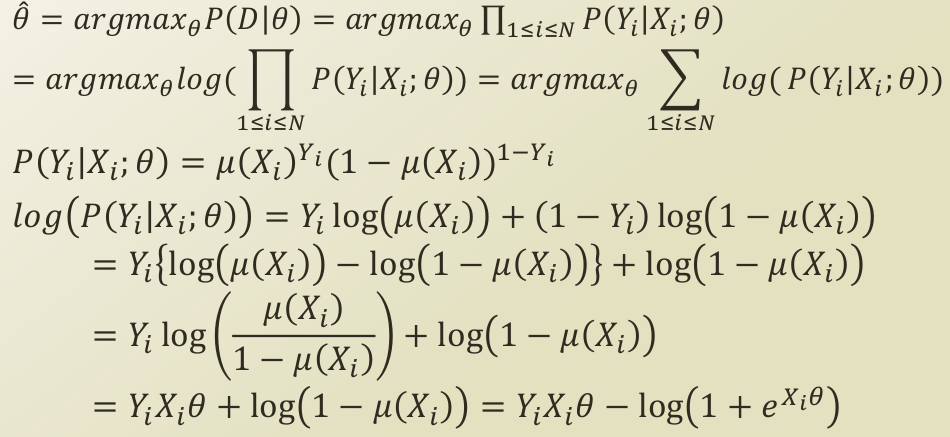
| P(Y | X)를 최적화하기 때문에, 이를 θ로 미분하게 되는데, 로지스틱 회귀는 binary classification 이기 때문에, bernoulli distribution을 P(Y | X)로 두고 최적화를 진행합니다. |
무엇보다 중요한 것은, 확률을 선형이 아닌, 확률의 공리를 충족하는 비선형 함수 logistic function을 가정하기 때문에, bernoulli distribution의 probability term에 logistic function을 대입해주어야 합니다.
최적화 과정은 김도형 박사님 블로그 가 개인적으로 이해하기 더 쉬워 이를 참고했는데요.

위에서 말씀드린 logistic_function을 확률값으로 대입해서 bernoulli distribution을 전개한 것입니다.
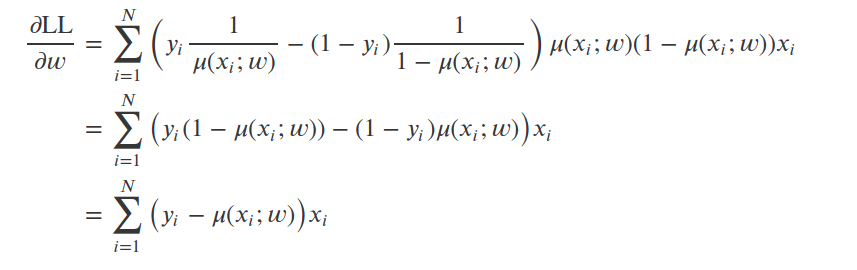
Log likelihood 를 미분의 chain rule 에 따라서 LL 에 대해 m(x_i;w) 로 미분해주고, m(x_i;w) 를 w로 미분하게 되어서 위와 같은 식이 나옵니다. 어떠한 w의 값이 딱 떨어져서 나오지 않네요. 이를 닫힌 값이 없다라고 합니다. 이에 따라 수치적 최적화(numerical optimization)을 통해 최적의 모수로 approximation 해야 합니다.
Numerical Optimization
저희는 LL 을 최대화했어야 했습니다. 근데 LL에 부호를 바꿔주게 되면 최소화시키는 최적화문제로 바뀌게 되었습니다. -LL을 w로 미분한 값에 learning rate이라는 hyper parameter 를 곱해주고 계속해서 w(모수)를 업데이트 시켜주면, 수치적 최적화 방법으로 최적 모수값을 구할 수 있게 됩니다. 이를 gradient descent 방법이라고 합니다. 보다 자세한 내용은 다음 포스팅에서 다루도록 하겠습니다.
Comments