나이브 베이즈 분류기 (Naive Bayes Classifier)
03 Jan 2019 | Machine_Learning HS
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
Why should we be Naive?
분류 문제를 풀기 위해서 머신 러닝 알고리즘을 적용하고, 해당 모델이 지도 학습 모형(supervised learning model)이라면, 학습 데이터로써, 특성 변수(입력 변수)와 그에 따른 라벨값이 주어져야 합니다. 이러한 데이터들로부터 우리가 알 수 있는 것은 아래와 같습니다.
- K개의 클래스 중 특정 클래스일 때, 입력 변수 X의 확률 P(X=x|Y=y)
- K개의 클래스 중 특정 클래스가 나올 확률 P(Y=y)
이들을 조합해보면, 베이즈 정리(Bayes Theorem)가 도출됩니다.
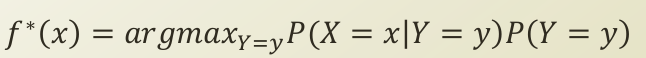
여기서 주목할 것은 바로 P(X=x|Y=y) 부분인데요. 입력 변수의 차원 d가 몇개인지에 따라서, 경우의 수가 기하급수적으로 증가하게 됩니다.(2^d-1)k 이에 따라서, joint probability 를 계산하는 데 있어, 연산의 부담이 증가하게 되는 것이죠. 안그래도 베이즈 정리에 따라 추론하는 MAP 추정이 많은 데이터를 필요로 하는데, 결합 확률 연산이 큰 부담이 되게 됩니다.
이에 따라 나온 가정이 바로 Conditional Independence 가정입니다. 흔히 Independence라 하면, P(X,Y) = P(X)P(Y) 로 정의되는데, 조건부 독립도 마찬가지입니다.

알아차리셨을꺼라 생각하지만, 곱셈을 의미하는, large pi 가 모수 추정에서 log likelihood 로써, log 가 씌워지면 덧셈이 되면서 계산이 용이하게 됩니다. 또한, 이에 따라 결합 확률 분포가 분해되어 멱함수였던 경우의 수가 (2-1)dk 로 줄어들게 되는 것이죠.
Various Naïve Bayes Classifier
나이브 베이즈 분류기는 입력 변수의 특징(X 벡터의 특징)에 따라 나뉘어질 수 있습니다.
GaussianNB: 가우시안 정규 분포 나이브 베이즈
BernoulliNB: 베르누이 분포 나이브 베이즈
MultinomialNB: 다항 분포 나이브 베이즈
X 벡터가 연속적(continous)이며, 클래스마다 특정한 값 주변에서 발견되는 경우에는 GaussianNB 를 따릅니다.
X 벡터가 binary value를 띄고 있을 때, BernoulliNB 를 따릅니다.
예로 들어 입력 변수의 차원이 [고객이 산 물건 , 고객이 반품한 물건] 이라고 했을 때, 트레이닝을 위해서 이를 one-hot-encoder로 펼치게 되면 [고객이 산 물건_1,…,고객인 산 물건_N , 고객이 반품한 물건_1,…,고객이 반품한 물건_M]이 될 것이고, 각 값들은 binary 값들을 가지고 있을 것입니다. 이 때, 특정 물건 몇 개를 사고, 특정 물건 몇 개를 반품했을 때, [0,0,1,0,1,0,1,..] 1번 고객으로 분류될 때입니다.
X 벡터가 Multinomial distribution 의 샘플을 따를 때, 위의 예시에서 고객이 마켓을 여러 번 왔다면, 여러개의 binary vector 가 중첩될 것이고 [[0,0,1,0,1,0,1,..],[0,0,1,0,1,0,1,..],[0,0,1,0,1,0,1,..]] 이에 따라 [1,3,7,2,0,2,…] 과 같은 단일 벡터로 나오게 되면, 이는 다항 분포를 따르는 입력 변수를 가지는 나이브 베이즈 분류 모델이라고 할 수 있습니다.
Problem of Naïve Bayes Classifier
- Naive Problem
- 모델의 이름에서도 알 수 있다시피, 가정이 매우 순진함을 알 수 있습니다. 입력 변수끼리 독립성을 가정함에따라, 다중 공선성(multi-collinearity) 와 같은 상황에서 가정이 무너질 수 있습니다.
- Incorrect Probability Estimations
- 관측치가 편향된 값이 나오게 되면, 모수의 추정값 또한 편향된 값이 나오게 됩니다.
- MLE 의 경우, 편향된 관측치에 대해 관측치(N)를 높이는 방법뿐이지만, MAP의 경우, prior 에 대한 올바른 정의가 요구됩니다.
본 포스팅은 카이스트 문일철 교수님의 강좌와 김도형 박사님의 블로그를 바탕으로 만들어졌습니다. 이미지 자료는 모두 문일철 교수님의 강좌 노트에서 첨부한 것입니다. 문제 시 바로 내리겠습니다.
본 포스팅은 단순히 개인 공부 정리 용도이며, 저자는 배경 지식이 많이 부족한 이유로, 최선을 다하겠지만 분명히 완벽하지 않거나, 틀린 부분이 있을 수 있습니다. 계속해서 수정해나가도록 하겠습니다.
Why should we be Naive?
분류 문제를 풀기 위해서 머신 러닝 알고리즘을 적용하고, 해당 모델이 지도 학습 모형(supervised learning model)이라면, 학습 데이터로써, 특성 변수(입력 변수)와 그에 따른 라벨값이 주어져야 합니다. 이러한 데이터들로부터 우리가 알 수 있는 것은 아래와 같습니다.
- K개의 클래스 중 특정 클래스일 때, 입력 변수 X의 확률 P(X=x|Y=y)
- K개의 클래스 중 특정 클래스가 나올 확률 P(Y=y)
이들을 조합해보면, 베이즈 정리(Bayes Theorem)가 도출됩니다.
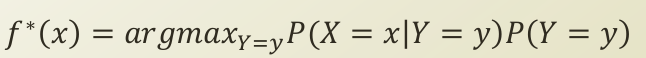
여기서 주목할 것은 바로 P(X=x|Y=y) 부분인데요. 입력 변수의 차원 d가 몇개인지에 따라서, 경우의 수가 기하급수적으로 증가하게 됩니다.(2^d-1)k 이에 따라서, joint probability 를 계산하는 데 있어, 연산의 부담이 증가하게 되는 것이죠. 안그래도 베이즈 정리에 따라 추론하는 MAP 추정이 많은 데이터를 필요로 하는데, 결합 확률 연산이 큰 부담이 되게 됩니다.
이에 따라 나온 가정이 바로 Conditional Independence 가정입니다. 흔히 Independence라 하면, P(X,Y) = P(X)P(Y) 로 정의되는데, 조건부 독립도 마찬가지입니다.

알아차리셨을꺼라 생각하지만, 곱셈을 의미하는, large pi 가 모수 추정에서 log likelihood 로써, log 가 씌워지면 덧셈이 되면서 계산이 용이하게 됩니다. 또한, 이에 따라 결합 확률 분포가 분해되어 멱함수였던 경우의 수가 (2-1)dk 로 줄어들게 되는 것이죠.
Various Naïve Bayes Classifier
나이브 베이즈 분류기는 입력 변수의 특징(X 벡터의 특징)에 따라 나뉘어질 수 있습니다.
GaussianNB: 가우시안 정규 분포 나이브 베이즈
BernoulliNB: 베르누이 분포 나이브 베이즈
MultinomialNB: 다항 분포 나이브 베이즈
X 벡터가 연속적(continous)이며, 클래스마다 특정한 값 주변에서 발견되는 경우에는 GaussianNB 를 따릅니다.
X 벡터가 binary value를 띄고 있을 때, BernoulliNB 를 따릅니다. 예로 들어 입력 변수의 차원이 [고객이 산 물건 , 고객이 반품한 물건] 이라고 했을 때, 트레이닝을 위해서 이를 one-hot-encoder로 펼치게 되면 [고객이 산 물건_1,…,고객인 산 물건_N , 고객이 반품한 물건_1,…,고객이 반품한 물건_M]이 될 것이고, 각 값들은 binary 값들을 가지고 있을 것입니다. 이 때, 특정 물건 몇 개를 사고, 특정 물건 몇 개를 반품했을 때, [0,0,1,0,1,0,1,..] 1번 고객으로 분류될 때입니다.
X 벡터가 Multinomial distribution 의 샘플을 따를 때, 위의 예시에서 고객이 마켓을 여러 번 왔다면, 여러개의 binary vector 가 중첩될 것이고 [[0,0,1,0,1,0,1,..],[0,0,1,0,1,0,1,..],[0,0,1,0,1,0,1,..]] 이에 따라 [1,3,7,2,0,2,…] 과 같은 단일 벡터로 나오게 되면, 이는 다항 분포를 따르는 입력 변수를 가지는 나이브 베이즈 분류 모델이라고 할 수 있습니다.
Problem of Naïve Bayes Classifier
- Naive Problem
- 모델의 이름에서도 알 수 있다시피, 가정이 매우 순진함을 알 수 있습니다. 입력 변수끼리 독립성을 가정함에따라, 다중 공선성(multi-collinearity) 와 같은 상황에서 가정이 무너질 수 있습니다.
- Incorrect Probability Estimations
- 관측치가 편향된 값이 나오게 되면, 모수의 추정값 또한 편향된 값이 나오게 됩니다.
- MLE 의 경우, 편향된 관측치에 대해 관측치(N)를 높이는 방법뿐이지만, MAP의 경우, prior 에 대한 올바른 정의가 요구됩니다.
Comments