Self-Paced Curriculum Learning
29 Jun 2019 | Deep_Learning HS
저희는 지금 커리큘럼 학습 영역에서 두 가지 방법론을 다루어 보았습니다. 첫 번째는 실험자가 사전 정보를 넣어주는 CL 두 번째는 일정 임계치를 넘어가면 샘플을 학습하는 SPL 이렇게 두 가지를 살펴보았는데요. 각각은 서로 다른 방법론을 사용하기 때문에, 각자의 장점이 있고 이에 따른 한계가 존재합니다. 이번 논문은 CL과 SPL 두 방법론을 결합한 SPCL 방법론을 다룬 Self-Paced Curriculum Learning 논문 에 대해 이야기해보겠습니다.
바로 본론으로 들어가보겠습니다. 각 방법론의 특성에 대해 정리한 아래의 표를 보면서 하나씩 뜯어보겠습니다.

우선 Comparable to human learning 부분을 보면, CL의 경우 실험자가 알려주는 방식입니다. 즉, 아이에게 부모님이 “이건 지지야!! 먹으면 안되!! 이건 먹어두 되요!!” 라고 경험(데이터)에 대해 알려주는 것과 같은 맥락입니다. Curriculum design 의 경우, 실험자가 학습 전에 미리 알려주기 때문에 사전 정보가 들어간다고 할 수 있습니다. 이에 따라, 휴리스틱한 접근 방법이라고 불리게 되는 것이죠.
SPL 의 경우, 학습자가 스스로 정의하는 방식입니다. 이전의 예를 들면, 아이가 이걸 먹어보니, 이건 영 먹을 것이 못된다. 저건 먹어보니 내 입맛에 딱 맞는다. 이런 식으로 스스로 점점 학습해나가면서 경험(데이터)에 대해 일정의 기준을 두고 학습하는 것을 의미합니다. Curriculum design 은 학습자가 학습을 하기 때문에 학습 자체를 목표로 하고, Gradient 를 통해, 학습이 됩니다.
SPCL은 이름에서 알 수 있다시피, 실험자와 학습자가 함께 학습해나가는 과정을 의미합니다. Curriculum design 을 보면, CL + SPL 의 디자인을 사용한다는 것을 알 수 있습니다. 여기서 주요 포인트는 training 방식은 Gradient 기반으로 SPL과 동일함을 알 수 있습니다.
이제 식을 통해서 SPCL가 어떠한 변화를 주면서 CL 과 SPL을 결합(collaborate) 했는지 알아보겠습니다.
아래의 식은 기존에 저희가 다뤘던 SPL에 대한 식입니다. 우변의 두 번째 term의 $-\lambda$ 는 $-\frac{1}{K}$ 와 같은 것으로, 보다 일반적으로는 $f(v;\lambda)$ 으로 표현할 수 있습니다.
아래의 식은 새롭게 다룰 SPCL에 대한 식입니다. 눈치채셨겠지만, $\Psi$ term이 생긴 것을 알 수 있습니다. 기존의 SPL 의 등식에서, CL의 사전 정보를 넣어주기 위해 추가한 term이 바로 $\Psi$ 가 되겠습니다.
그렇다면 $\Psi$ 는 무엇을 의미할까요? 이는 Curriculum Region 을 의미합니다. 보다 쉽게 표로 설명을 드리겠습니다.

기존의 SPL은 특정 임계값(indicator function $\psi$) 을 넘는 데이터 $x_{i}$ 의 weight variable $v_{i}$에 1을 주고 아닌 경우, 0을 주는 binary 방식으로 커리큘럼을 진행해왔습니다. SPCL의 경우, 처음에 실험자가 각 데이터 $x_{i}$ 에 대해서, 1부터 데이터 갯수 $n$ 까지 순서를 매겨줍니다. 이를 수식으로 $\gamma(x_{i})$ 로 표현하는데 이 값은 rank 라고 생각하시면 편할 것 같습니다. 즉, 작을 수록 먼저 학습되는 easy sample 입니다. 이 rank 값은 Curriculum region $\Psi$ 를 한정하는 데에 사용됩니다. 우선, 논문 내의 Definition 부터 보면 아래와 같습니다.
무슨 말인가 곰곰히 살펴보면, rank 가 높을 수록 즉, 데이터 $x_{i}$에 대한 $\gamma$ 값이 작을 수록, 데이터의 가중치 변수 $v_{i}$의 기댓값이 높게 형성되는 영역을 의미합니다. 위의 사진을 보시면, 이전의 SPL의 경우 모든 $v_{i}$ 은 0 또는 1의 값을 가지게 됨으로써, easy sample 이라고 해서 데이터의 묶음이 학습될 때, 같은 가중치인 1로 학습이 되었다면, 이제 실험자가 정한 rank에 따라 그 가중치가 변하게 되어, 모델에 학습이 된다 라는 것이 됩니다.
Curriculum region 을 어떻게 정해는지에 대해서는 크게 어렵지 않습니다. 아래의 식에서 $a$는 $\gamma$ 를 대표하며, $c$ 는 상수입니다. 해석해보면, rank 가 낮을 수록, $v$ 의 region은 더욱 커지게 되고, 이는 rank $\gamma$ 와 선형의 관계를 가지고 있다. 라고 할 수 있습니다.
주목할 점은, 이러한 Curriculum region에 따라 유도되는 $v_{i}$ 는 실제 학습 프로세스에서 약한 영향만을 끼치게 됩니다. 그 이유는 처음에 [1,1,1]으로 주어지던 $(v_{1},v_{2},v_{3})$ 가 prior information 을 통해 [0.5,0.3,0.2] 로 주어졌다고 해도, 결국 모델의 학습 과정을 통해서 해당 region 은 크게 변화하게 될 것이기 때문입니다. 이에 따라서, $\Psi$ 에 따른 Curriculum region 은 $v_{i}$ 의 initialize 의 효과를 가진다 라고 할 수 있습니다.

위의 표는 알고리즘을 나타내는데, 1번의 Curriculum region $\Psi$ 를 유도하는 과정 이외에는 alternative search strategy 방식으로 $w,v$ 중 하나를 고정하고 나머지 하나를 최적화하는 방법을 사용하는 것은 이전의 SPL과 동일합니다.
마지막으로 Self-paced function 에 다양한 활용에 대해서 알아보도록 하겠습니다.
첫 번째는 저희가 여태 써왔던 norm 1 을 사용한 self-paced function입니다. SPL에서는 hard 방식으로 $v_{i}$ 에서는 binary 값만 가질 수 있게끔 설정되었습니다.
두 번째는 linear scheme 이라고 불리는 함수로, soft 을 사용합니다.
세 번째 방식은 lienar scheme보다 더 보수적인 방식으로 로그를 사용하는 logarithmic scheme 입니다.
$\zeta = 1-\lambda$ 이며, $0 < \lambda < 1$ 의 조건을 가집니다.
마지막으로 hard 방식과 soft 방식을 혼합한 Mixture scheme 이 있습니다. 모델의 loss 가 너무 커질 경우, hard 방식을 사용하고 나머지의 경우에는 soft 방식이 사용 가능하게끔 설계되었다고 합니다.
Self-paced function implement 에 대한 보다 깊은 수학적 과정에 관심있으신 분들은 해당 링크 를 참고하시면 좋을 것 같습니다.
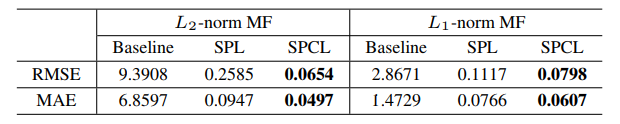
해당 방법론을 Matrix Formulation 에 적용한 후, RMSE 와 MAE로 성과 평과를 한 표를 끝으로 포스팅을 마무리하도록 하겠습니다!
저희는 지금 커리큘럼 학습 영역에서 두 가지 방법론을 다루어 보았습니다. 첫 번째는 실험자가 사전 정보를 넣어주는 CL 두 번째는 일정 임계치를 넘어가면 샘플을 학습하는 SPL 이렇게 두 가지를 살펴보았는데요. 각각은 서로 다른 방법론을 사용하기 때문에, 각자의 장점이 있고 이에 따른 한계가 존재합니다. 이번 논문은 CL과 SPL 두 방법론을 결합한 SPCL 방법론을 다룬 Self-Paced Curriculum Learning 논문 에 대해 이야기해보겠습니다.
바로 본론으로 들어가보겠습니다. 각 방법론의 특성에 대해 정리한 아래의 표를 보면서 하나씩 뜯어보겠습니다.

우선 Comparable to human learning 부분을 보면, CL의 경우 실험자가 알려주는 방식입니다. 즉, 아이에게 부모님이 “이건 지지야!! 먹으면 안되!! 이건 먹어두 되요!!” 라고 경험(데이터)에 대해 알려주는 것과 같은 맥락입니다. Curriculum design 의 경우, 실험자가 학습 전에 미리 알려주기 때문에 사전 정보가 들어간다고 할 수 있습니다. 이에 따라, 휴리스틱한 접근 방법이라고 불리게 되는 것이죠.
SPL 의 경우, 학습자가 스스로 정의하는 방식입니다. 이전의 예를 들면, 아이가 이걸 먹어보니, 이건 영 먹을 것이 못된다. 저건 먹어보니 내 입맛에 딱 맞는다. 이런 식으로 스스로 점점 학습해나가면서 경험(데이터)에 대해 일정의 기준을 두고 학습하는 것을 의미합니다. Curriculum design 은 학습자가 학습을 하기 때문에 학습 자체를 목표로 하고, Gradient 를 통해, 학습이 됩니다.
SPCL은 이름에서 알 수 있다시피, 실험자와 학습자가 함께 학습해나가는 과정을 의미합니다. Curriculum design 을 보면, CL + SPL 의 디자인을 사용한다는 것을 알 수 있습니다. 여기서 주요 포인트는 training 방식은 Gradient 기반으로 SPL과 동일함을 알 수 있습니다.
이제 식을 통해서 SPCL가 어떠한 변화를 주면서 CL 과 SPL을 결합(collaborate) 했는지 알아보겠습니다.
아래의 식은 기존에 저희가 다뤘던 SPL에 대한 식입니다. 우변의 두 번째 term의 $-\lambda$ 는 $-\frac{1}{K}$ 와 같은 것으로, 보다 일반적으로는 $f(v;\lambda)$ 으로 표현할 수 있습니다.
아래의 식은 새롭게 다룰 SPCL에 대한 식입니다. 눈치채셨겠지만, $\Psi$ term이 생긴 것을 알 수 있습니다. 기존의 SPL 의 등식에서, CL의 사전 정보를 넣어주기 위해 추가한 term이 바로 $\Psi$ 가 되겠습니다.
그렇다면 $\Psi$ 는 무엇을 의미할까요? 이는 Curriculum Region 을 의미합니다. 보다 쉽게 표로 설명을 드리겠습니다.

기존의 SPL은 특정 임계값(indicator function $\psi$) 을 넘는 데이터 $x_{i}$ 의 weight variable $v_{i}$에 1을 주고 아닌 경우, 0을 주는 binary 방식으로 커리큘럼을 진행해왔습니다. SPCL의 경우, 처음에 실험자가 각 데이터 $x_{i}$ 에 대해서, 1부터 데이터 갯수 $n$ 까지 순서를 매겨줍니다. 이를 수식으로 $\gamma(x_{i})$ 로 표현하는데 이 값은 rank 라고 생각하시면 편할 것 같습니다. 즉, 작을 수록 먼저 학습되는 easy sample 입니다. 이 rank 값은 Curriculum region $\Psi$ 를 한정하는 데에 사용됩니다. 우선, 논문 내의 Definition 부터 보면 아래와 같습니다.
무슨 말인가 곰곰히 살펴보면, rank 가 높을 수록 즉, 데이터 $x_{i}$에 대한 $\gamma$ 값이 작을 수록, 데이터의 가중치 변수 $v_{i}$의 기댓값이 높게 형성되는 영역을 의미합니다. 위의 사진을 보시면, 이전의 SPL의 경우 모든 $v_{i}$ 은 0 또는 1의 값을 가지게 됨으로써, easy sample 이라고 해서 데이터의 묶음이 학습될 때, 같은 가중치인 1로 학습이 되었다면, 이제 실험자가 정한 rank에 따라 그 가중치가 변하게 되어, 모델에 학습이 된다 라는 것이 됩니다.
Curriculum region 을 어떻게 정해는지에 대해서는 크게 어렵지 않습니다. 아래의 식에서 $a$는 $\gamma$ 를 대표하며, $c$ 는 상수입니다. 해석해보면, rank 가 낮을 수록, $v$ 의 region은 더욱 커지게 되고, 이는 rank $\gamma$ 와 선형의 관계를 가지고 있다. 라고 할 수 있습니다.
주목할 점은, 이러한 Curriculum region에 따라 유도되는 $v_{i}$ 는 실제 학습 프로세스에서 약한 영향만을 끼치게 됩니다. 그 이유는 처음에 [1,1,1]으로 주어지던 $(v_{1},v_{2},v_{3})$ 가 prior information 을 통해 [0.5,0.3,0.2] 로 주어졌다고 해도, 결국 모델의 학습 과정을 통해서 해당 region 은 크게 변화하게 될 것이기 때문입니다. 이에 따라서, $\Psi$ 에 따른 Curriculum region 은 $v_{i}$ 의 initialize 의 효과를 가진다 라고 할 수 있습니다.

위의 표는 알고리즘을 나타내는데, 1번의 Curriculum region $\Psi$ 를 유도하는 과정 이외에는 alternative search strategy 방식으로 $w,v$ 중 하나를 고정하고 나머지 하나를 최적화하는 방법을 사용하는 것은 이전의 SPL과 동일합니다.
마지막으로 Self-paced function 에 다양한 활용에 대해서 알아보도록 하겠습니다.
첫 번째는 저희가 여태 써왔던 norm 1 을 사용한 self-paced function입니다. SPL에서는 hard 방식으로 $v_{i}$ 에서는 binary 값만 가질 수 있게끔 설정되었습니다.
두 번째는 linear scheme 이라고 불리는 함수로, soft 을 사용합니다.
세 번째 방식은 lienar scheme보다 더 보수적인 방식으로 로그를 사용하는 logarithmic scheme 입니다. $\zeta = 1-\lambda$ 이며, $0 < \lambda < 1$ 의 조건을 가집니다.
마지막으로 hard 방식과 soft 방식을 혼합한 Mixture scheme 이 있습니다. 모델의 loss 가 너무 커질 경우, hard 방식을 사용하고 나머지의 경우에는 soft 방식이 사용 가능하게끔 설계되었다고 합니다.
Self-paced function implement 에 대한 보다 깊은 수학적 과정에 관심있으신 분들은 해당 링크 를 참고하시면 좋을 것 같습니다.
해당 방법론을 Matrix Formulation 에 적용한 후, RMSE 와 MAE로 성과 평과를 한 표를 끝으로 포스팅을 마무리하도록 하겠습니다!

Comments